Анализ - поведение - материал
Cтраница 1
 |
Схематическое представление поверхностей разрушения профиля вязких ( а и хрупких ( б усталостных бороздок. [1] |
Анализ поведения материала с трещиной при циклическом нагружении требует учета контролирующего скорость роста трещины микромеханизма, так как при реализации одного и того же макромеханизма ( например, типа 1) могут наблюдаться различные микромеханизмы усталостного разрушения: квазивязкий отрыв - усталостные вязкие бороздки и квазихрупкий отрыв - усталостные хрупкие бороздки ( рис. 37), вязкий отрыв - ямочное разрушение, межзеренный хрупкий отрыв, внутризеренный хрупкий отрыв - скол. [2]
Анализ поведения материала с трещиной при циклическом нагружении требует учета контролирующего скорость роста трещины микромеханизма [42, 48, 49], При реализации одного и того же макромеханизма ( например, тип I) могут наблюдаться различные микромеханизмы усталостного разрушения: квазивязкий отрыв-усталостные вязкие бороздки, квазихрупкий отрыв-усталостные хрупкие бороздки, вязкий отрыв-ямочное разрушение, межзеренный хрупкий отрыв. [3]
Сложность анализа поведения материала в этих зонах и выведения математических зависимостей заключается в том, что термопластичный материал находится в них не полностью в расплавленном состоянии. [4]
К анализу поведения материала при высокой скорости деформации целиком относится то, что сказано в § 1 предыдущей главы о свойствах материала в зависимости от времени. Из попыток детального объяснения влияния скорости деформации приведем только выдвинутое недавно объяснение запаздывания текучести в мягкой стали. Чтобы эти дислокации начали двигаться, надо приложить извне некоторое напряжение, равное пределу текучести. Но в углеродистых сталях каждая дислокация окружена облаком атомов углерода, которое препятствует перемещению дислокаций. Поэтому требуется еще некоторое добавочное внешнее напряжение, чтобы освободить дислокации от облаков углерода. Этим объясняют наличие у мягких сталей и железа верхнего и нижнего пределов текучести. [5]
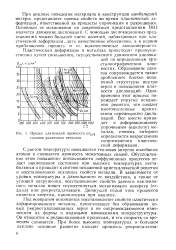 |
Предел длительной прочности ( ттпз талла. [6] |
При анализе поведения материала в конструкции наибольший интерес представляет оценка свойств во время пластической деформации, ответственной за процессы упрочнения и разрушения. Основным ее механизмом по современным представлениям [83] является движение дислокаций. [7]
При анализе поведения материала в области 1 должны применяться уравнения состояния вязкоупругого тела, деформируемого без течения ( см. гл. [8]
Приведенный выше анализ поведения микронеоднородного материала при растяжении - сжатии основывался на наглядной интерпретации в виде стержневой модели Мазинга. Полученные соотношения могут быть, однако, непосредственно распространены на пропорциональное нагружение при произвольном виде напряженного состояния. Формальное обобщение на условия непропорционального нагружения требует уже перехода к операциям с тензорами. Полученная таким путем структурная модель среды должна рассматриваться как математическая модель, имеющая механический ( стержневой) аналог лишь в самом простом случае. [9]
Более строгой проверкой модели может служить анализ поведения материала при меняющейся скорости экструзии. На рис. 1.30 сопоставлены экспериментальные и вычисленные зависимости р - In vf для двух материалов. При низких экструзионных отношениях у обоих материалов расчетные значения угла наклона кривых р - In vf хорошо согласуются с экспериментальными, но модель с р О не предсказывает быстрого подъема функции, который наблюдается при высоких экструзионных отношениях. [10]
Конкретные виды реологических уравнений состояния, связыва - ющих кинематические переменные ( деформация, скорость деформации) и переменные статической природы ( напряжение, скорость напряжения), вытекают либо из молекулярных теорий, построенных на основании анализа поведения материалов определенной внутренней структуры, либо при рассмотрении различных реологических моделей с учетом общих принципов механики сплошной среды. Пригодность этих уравнений оценивается путем сопоставления их с экспериментами и по общим закономерностям механического поведения данного класса материалов. [11]
Теории разрушения, базирующиеся на положениях механики сплошной среды, основаны на том, что поведение материала или конструкции под нагрузкой можно предсказать по данным испытаний на растяжение ( или подобных им), исходя из предположения, что материал является однородным. Анализ поведения материала при наличии концентраторов напряжений ( типа трещин и надрезов) на основе существующей теории прочности и пластичности затруднен, так как при возникновении повреждений материал становится неоднородным. Более того, в различных объемах нагружаемого тела и особенно вблизи края трещины материал деформируется с различной скоростью, что трудно учесть на основе теории сплошной среды. [12]
Поскольку одной из основных задач любой теории деформирования является расчет конструкций в эксплуатационных условиях, отмеченная близость кривых деформирования идеально вязких подзлементов к диаграмме идеальной пластичности будет иметь немаловажное значение в ходе дальнейшего изложения. Отсюда, как будет показано, вытекают возможности для существенного упрощения анализа поведения материалов и конструкций. С другой стороны, различие между двумя видами неупругой деформации - склерономной ( пластической) и реономной ( вязкой) в свете рассматриваемой теории микронеоднородной среды оказывается непринципиальным ( этот вопрос более подробно будет проанализирован в гл. [13]
За последние годы развитие получила линейная механика разрушения ( или механика хрупкого разрушения), концепции которой используются для анализа поведения материалов в условиях хрупкого разрушения. Здесь достаточно только сказать, что в основном эти концепции содержат ряд положений, позволяющих анализировать напряжения, при которых происходит мгновенное разрушение вследствие наличия трещинообразного дефекта в материале. При этом принимается во внимание характер внешних нагрузок, размер объема, размер и форма дефекта. [14]
За последнее время написано несколько обстоятельных обзоров [73-75] о влиянии растворенных атомов на механические свойства сплавов. Хотя в большинстве из их рассматривается поведение альфа-твердых растворов при низких температурах, некоторые положения применимы и для высокотемпературной ползучести. С другой стороны, относительная роль различных механизмов упрочнения изменяется с увеличением температуры службы, поэтому для анализа поведения материала при высоких температурах приходится вводить новые факторы. [15]
Страницы: 1 2