Обработка - символ
Cтраница 1
Обработка символов с помощью программ PUTC и GETC за один прогон не так уж и плоха, как можно было бы подумать. [1]
 |
Пример программирования универсального адаптера интерфейса. [2] |
После обработки символов производится возврат к началу программы ввода. Если в заданный интервал времени последующие символы не приходят, то программа ввода заканчивается. [3]
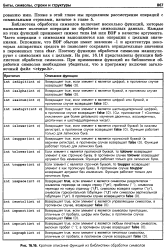 |
Краткое описание функций из библиотеки обработки символов. [4] |
Библиотека обработки символов включает несколько функций, которые выполняют полезные операции по обработке символьных данных. Каждая из этих функций принимает символ типа int или EOF в качестве аргумента. Часто операции с символами выполняются как операции с целыми значениями. Вспомним, что EOF обычно имеет значение - 1 и архитектура некоторых аппаратных средств не позволяет сохранять отрицательные значения в переменных типа char. Поэтому функции обработки символов манипулируют с символами как с целыми. На рис. 16.16 представлены функции библиотеки обработки символов. [5]
 |
Информация о составе оборудования ЭВМ, возвращаемая в регистре АХ при прерывании И. [6] |
Процедуры обработки символов передают символы на экран и обратно. Процедуры графического интерфейса изображают и считывают точки графического изображения и изменяют цвета. [7]
Библиотека обработки символов включает в себя несколько функций, выполняющих ряд полезных проверок и операций с символьными данными. Как мы уже говорили в 4 - й главе, операции с символами часто выполняются как с целыми числами, поскольку символ в С это однобайтовое целое. Вспомните, что EOF обычно имеет значение - 1, а архитектура некоторых аппаратных средств не позволяет запоминать отрицательные значения в переменных типа char. Следовательно, функции обработки символов оперируют с символами как с целыми числами. На рис. 8.1 приведен перечень функций библиотеки обработки символов. [8]
Отсутствие обработки символа новой строки при вводе, если символы читаются по одному, может привести к логической ошибке. [9]
Отсутствие обработки символов новой строки во входном потоке при чтении символов по одному может приводить к логическим ошибкам. [10]
На этом обработка символа then заканчивается. [11]
В режиме обработки символов числовые значения произведений координаты узловой точки на тригонометрическую функцию заданного угла заранее подсчитаны и сведены в таблицу, реализованную аппаратным образом. [12]
Рекурсия широко применяется при обработке символов. В качестве примера мы рассмотрим здесь обработку алгебраических выражений. Эти выражения состоят из наименований переменных, а также из знаков операций и скобок. Мы будем обозначать переменные одиночными буквами. [13]
Рекурсия широко применяется при обработке символов. Эти выражения состоят из наименований переменных, а также из знаков операций и скобок. Мы будем обозначать переменные одиночными буквами. [14]
Это правило предохраняет М от бесконечной обработки вводного символа. [15]
Страницы: 1 2 3 4