Статистическая обработка - выборка
Cтраница 1
Статистическая обработка выборок, содержащих некоторое число пустых проб, обусловленных нижним пределом определений, всегда сопряжена с некоторыми трудностями в связи с недостаточной разработкой критериев, связывающих параметры исходной и неполно определенной выборок с метрологическими характеристиками метода анализа. С помощью МЭСМ на различных моделях распределений, охватывающих содержания ниже предела обнаружения метода анализа, изучается вся гамма возможных вариантов исходное распределение - неполно определенная выборка и создается предпосылка для дальнейшего удовлетворительного решения обратных задач. [1]
Однако совместная статистическая обработка выборок может быть корректна только в том случае, если различия между ними носят случайный характер и они являются приближенной оценкой одной генеральной совокупности. Такие выборки называют равноточными, а полученное в результате совместной обработки стандартное отклонение называют средневзвешенным стандартным отклонением. Пример такого сравнения будет рассмотрен ниже. [2]
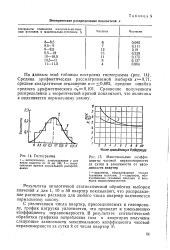 |
Максимальные коэффициенты часовой неравномерности за сутки в зависимости от населенности квартир. [3] |
Результаты аналогичной статистической обработки выборок значений х для 1, 10 и 50 квартир показывают, что распределение расчетных расходов для любого числа квартир подчиняется нормальному закону. [4]
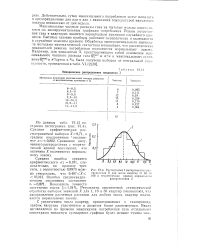 |
Эмпирическое распределение показателя А.| Гистограмма / эмпирического распределения А для числа квартир от 50 до 100 и теоретическая кривая нормального распределения 2. [5] |
Результаты аналогичной статистической обработки выборок значений X для 1, 10 и 50 квартир показывают, что распределение расчетных расходов для любого числа квартир подчиняется нормальному закону. [6]
Результаты, полученные при статистической обработке выборки, будут достоверны только в том случае, если выборка однородна, т.е. если варианты, входящие в нее, не отягощены грубыми ошибками, допущенными при измерении или расчете. Такие варианты должны быть исключены из выборки перед окончательным вычислением ее статистических характеристик. [7]
Одним из полезнейших изобретений для статистической обработки выборок является вероятностная бумага. [8]
Таким образом, метод Монте-Карло предполагает использование двух моделей газопровода: вероятностной-для построения случайной выборки состояний и гидравлической - для построения выборки значений пропускной способности как функции состояния. Кроме того, должен существовать блок статистической обработки последней выборки, который и определяет показатели надежности. В этой модификации метода пропускная способность рассматривается как случайная величина. Последовательность изменений состояния и пропускной способности во времени игнорируется. Вероятность данного состояния интерпретируется как доля рассматриваемого периода времени, когда реализуется данное состояние. [9]
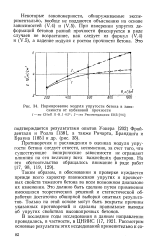 |
Нормирование модуля упругости бетона в зависимости от кубиковой прочности. [10] |
Таким образом, в обосновании и проверке нуждается прежде всего характер взаимосвязи упругих и прочностных свойств тяжелого бетона во всем возможном диапазоне их изменения. Это должно быть сделано путем применения имеющихся теоретических решений и статистической обработки достаточно обширной выборки опытных результатов. Только на этой основе могут быть вскрыты причины указанных противоречий и сделаны правильные выводы об упругих свойствах высокопрочных бетонов. [11]
В работе [109] не указывается, каким образом определяется и корректируется смещенность получаемой оценки ( аналог систематической погрешности), поскольку отказ от понятия истинное значение исключает такую возможность. Не указано также, каким образом учитывать при оценивании неопределенности измерений по типу А изменение измеряемой величины в процессе формирования необходимой для статистической обработки выборки результатов измерений, если такое изменение имеет место. [12]
Модели множественного выбора ( multiple choice model), имеющие более чем две альтернативы, строятся на основе моделей бинарного выбора. При этом множественный выбор может быть представлен как последовательность бинарных выборов. Обобщением биномиального распределения на случай более чем двух возможных исходов является полиномиальный ( мультиномиальный) закон распределения. Полиномиальное распределение используется при статистической обработке выборок большой совокупности, элементы которой разделяются более чем на две категории, применяются в социологических, социально-экономических и медицинских выборочных обследованиях. [13]
Страницы: 1