Анализ - процесс - ректификация
Cтраница 2
В настоящее время решению данной проблемы уделяется очень большое внимание, что является следствием необходимости разработки наиболее эффективных методов анализа процесса ректификации многокомпонентных смесей. К сожалению, известно лишь небольшое число таких систем программ [130, 135, 276] и публикации [268, 269, 277] о многих из них носят рекламный характер. [16]
Вопросам расчета и анализа узлов ректификации воздуха в книге уделено основное внимание по следующим причинам: в современных крупных ВРУ построение узла ректификации оказывает основное влияние на их показатели; вопросы анализа процесса ректификации воздуха в большинстве книг по криогенной технике освещены менее полно, чем вопросы анализа холодильных циклов; при расчете ВРУ уравнения для узла ректификации целесообразно составлять на основе соотношений, полученных в результате предварительных расчетов и анализа этого узла. [17]
Если учесть все недостатки данной системы программ, то становится очевидным, что она может быть использована для решения ограниченного круга задач и не может быть рекомендована для создания автоматизированных систем синтеза и анализа процессов ректификации. [18]
Анализ процессе совмещенной конденсации и испарения смеси можно успешно проводить с помощью комбинированной энтальпийной и изобарной диаграммы, уравнения рабочей линии и кривой равновесия фаз, а также на основе других закономерностей, используемых при анализе процесса ректификации. [19]
Анализ процесса совмещенной конденсации и испарения смеси можно успешно проводить с помощью комбинированной энталышйной и изобарной диаграммы, уравнения рабочей линии и кривой равновесия Фаз, а также на основе других закономерностей, используемых при анализе процесса ректификации. [20]
Соотношение (VII.78) пригодно для анализа характера изменения величины ВЭТТ. При анализе процесса ректификации в насадочных колоннах с использованием диффузионной модели было установлено, что чем больше относительная летучесть, тем сильнее проявляется зависимость ВЕП и ВЭТТ от молярного состава компонентов, которая больше для ВЕП, чем для ВЭТТ. При этом значения ВЕП и ВЭТТ изменяются по высоте колонны. [21]
Наиболее существенной чертой случаев второго типа является наличие на ректификационной диаграмме разделяющих поверхностей между областями ректификации с различными первыми фракциями. Для тех систем, в которых подобные разделяющие поверхности оказываются плоскими, анализ процессов ректификации практически не имеет особенностей, по сравнению со случаями первого типа, рассмотренными выше. Напротив, при искривленности разделяющих поверхностей, как и в тройных системах, протекание ректификации усложняется и зависит от характера кривизны и относительного расположения особых точек системы. [22]
Выражение ( 1) справедливо для закрытой непроточной системы, внутри которой отсутствуют фазовые превращения. Несмотря на такие существенные ограничения, уравнение ( 1) используется рядом авторов 3 3 для анализа процесса ректификации. [23]
Процесс ректификации при бесконечной разделительной способности, как и процесс обратимой ректификации, полностью определяется структурой концентрационного симплекса. Однако если при анализе процесса обратимой ректификации определяющую роль играют а-много-образия ( границы областей обратимой ректификации) и направление ноды жидкость - пар в точке питания, то в случае анализа процесса ректификации при бесконечной разделительной способности такую роль играют положения особых точек в концентрационном симплексе, связи между этими точками согласно структурной матрице и положения границ областей ректификации. Если анализ возможных составов продуктов обратимой ректификации требует обязательного использования модели фазового равновесия, то аналогичный анализ для процесса при бесконечной разделительной способности в ряде случаев возможен с применением только структурной матрицы и данных по составам сырья и азеотропов. В разделе 9 дан общий подход к анализу многообразия возможных составов продуктов разделения азеотропных смесей в одной колонне. [24]
Более сложный характер могут иметь процессы ректификации, когда в тройной системе оказывается не менее двух особых точек с минимальными температурами кипения относительно своей окрестности. В подобных случаях на диаграмме дистилляционных линий имеется не менее двух неустойчивых узлов, что может наблюдаться лишь при наличии в системе или бинарных азеотропов типа s2, или тройных седловых азеотропов, поскольку только этими азеотропами могут быть образованы дистилляционные линии, разделяющие области дистилляции с разными неустойчивыми узлами. Здесь для анализа процессов ректификации можно использовать тот же подход, однако ввиду более сложного характера этих случаев целесообразно рассмотреть примеры, вскрывающие основные особенности. [25]
Де-Минье [109], Ивела и Велча [110], И. Н. Бушмакина и И. Н. Киша [111, 112] и целый ряд других многочисленных работ. Результаты работ в указанном направлении позволяют построить общий метод анализа процессов ректификации, причем этот метод может находить применение в разном плане, а именно: 1) для объяснения в рамках определенной схемы закономерностей, наблюдаемых экспериментально; 2) для установления возможных результатов ректификации на основе данных о фазовых равновесиях; 3) для целенаправленного планирования ректификационных опытов и интерпретации их результатов. [26]
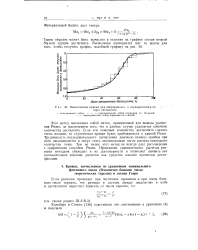 |
Вычисленные кривые для непрерывного и периодического от -.. [27] |
Этот метод напоминает собой метод, примененный для вывода уравнения Рэлея, за исключением того, что в данном случае удаляются конечные количества дестиллята. Трудоемкость последовательного вычисления довольно велика; ошибки при этом накапливаются и могут стать значительными после расчета некоторого количества точек. Тем не менее этот метод не всегда дает расхождения с графическим способом Рэлея. Проведение сравнительных расчетов разными методами убеждает в их достоверности и позволяет выявить все положительное значение расчетов как средства анализа процессов ректификации. [28]
Страницы: 1 2