Анализ - статический режим
Cтраница 1
Анализ статических режимов сводится к решению систем АУ. Для решения АУ применяют итерационные методы, основные характеристики которых - сходимость и скорость сходимости к точному решению. В САПР применяют в основном методы простой итерации, Ньютона и релаксационные. Методы простой итерации и релаксационные имеют линейную скорость сходимости и требуют небольших вычислительных затрат на одну итерацию. Эти методы применяются в основном для решения систем АУ большой размерности. Метод Ньютона имеет квадратичную скорость сходимости, но в общем случае сходится только в окрестности точного решения. Для расширения области сходимости метода Ньютона применяются метод продолжения решения по параметру и метод дифференцирования по параметру. Метод Ньютона и его модификации сводятся к решению систем ЛАУ на каждой итерации. Для решения систем ЛАУ наиболее широко применяют метод Гаусса и LU-разложения. Для систем ЛАУ большой размерности эти методы эффективны только при учете разреженности матриц коэффициентов. [1]
Анализ статического режима комбинированного переключателя дает возможность рассчитать его параметры исходя из оптимальных условий, которые обеспечивают стабильность выходных импульсов и уменьшение расходуемой мощности. [2]
Однако анализ статических режимов при бесконечно медленном изменении амплитуды сигнала является недостаточным. При этом даже в случае простейшего С-фильтра в системе АРУ анализ не всегда удается довести до конца, так как процессы в системе описываются в общем случае нелинейным дифференциальным уравнением. В случае линеаризации зависимости коэффициента усиления от регулирующего напряжения линейное уравнение процесса регулирования имеет переменные коэффициенты, и только в отдельных частных случаях его решение может быть представлено в удобном для практике виде. [3]
 |
Структура биполярного транзистора ( а и МДП-транзистора ( б. [4] |
При анализе статических режимов система аналогичного вида получается для каждого набора внешних смещений на выводах прибора. [5]
При анализе статического режима будем предполагать, что амплитуды напряжений u V и u2U2 изменяются весьма медленно и переходные процессы в системе не имеют сколько-нибудь существенного значения. [6]
При анализе статических режимов работы транзистора удобно пользоваться формулами Эберса - Молла, которые содержат нормальные и инверсные значения параметров и пригодны для любого сочетания полярностей напряжений на переходах. [7]
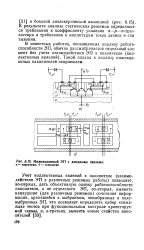 |
Инжекционный ЭП с диодными связями. а - структура, б - топология. [8] |
В результате анализа статических режимов определяются требования к коэффициенту усиления п - р-п-трап-зистора и требования к амплитудам токов записи и счи тывания. [9]
 |
Схема замещения асинхронного двигателя при переменной частоте питающего напряжения. [10] |
Часто для упрощения анализа статических режимов используют Г - образную схему замещения, для чего подключают контур намагничивания непосредственно к зажимам питающего напряжения, что не вносит существенных погрешностей в расчеты. [11]
Результаты описанного выше анализа статических режимов инжекционных накопителей позволяют определить условия работоспособности ЭП с инжекционным питанием, провести сравнительный анализ ЭП, выделить трудно контролируемые параметры, к разбросу которых наиболее чувствительны накопители, оценить величины управляющих сигналов с учетом изменения этих параметров, выбрать наиболее приемлемые способы записи и считывания накопителя. [12]
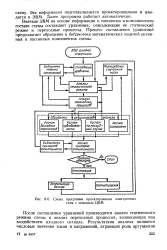 |
Схема программы проектирования электронных схем с помощью ЦВМ. [13] |
После составления уравнений производятся анализ статического режима схемы и анализ переходных процессов, возникающих под воздействием входного сигнала. [14]
В конкретном случае, для анализа статических режимов ФСН приняты следующие допущения. [15]
Страницы: 1 2