Анализ - сложность
Cтраница 1
Анализ сложности обычно применяют к конкретным алгоритмам, но его можно применить также и к общим задачам. В этом случае определяется нижняя оценка сложности из всех алгоритмов, решающих задачу. Это обеспечивает значение сложности, не зависящее от алгоритма, и, кроме того, может оказаться полезным в доказательстве того, что данный алгоритм оптимален ( с точностью до константы), и в определении случаев, когда дальнейшая работа может привести к лучшему алгоритму решения задачи. [1]
Анализ сложности рекурсивных алгоритмов затронут в основном тексте книги Макконелла, однако для получения функции трудоемкости необходим более детальный анализ, учитывающий трудоемкость вызова рекурсивной функции и количество вершин рекурсивного дерева. [2]
Для анализа сложности геологических условий целесообразно среди применявшихся КНБК выбрать компоновки, ука занные в подписях к рисункам приложения. [3]
Требуется сделать анализ сложности структуры малой системы - фирмы численностью 5 человек, оказывающей посреднические услуги в области перевозки малогабаритных грузов. Структура фирмы: администрация; бухгалтерия; отдел маркетинга; технический отдел; производственный отдел; финансовый отдел; гараж; диспетчерская; отдел кадров. Она должна разработать положения о своих подразделениях, вести планирование, учет и контроль выполняемых работ и их оплату. Очевидно, что 9 подразделений на 5 человек - надуманная структура фирмы, отвечающая требованиям моды, но не рациональности структуры и экономии средств. На практике на раннем этапе строительства рыночных отношений зачастую структуры фирм отвечают в большей мере не требованиям экономики, а амбициям инвесторов. [4]
Для проведения анализа сложности этого алгоритма необходимо определить, сколько раз вызывается каждая из четырех процедур рисования кривых. [5]
Использование математических методов анализа сложности поведения человека и животных с помощью современной компьютерной техники дает возможность более глубоко и всесторонне вскрыть механизмы регуляции физиологических функций. [6]
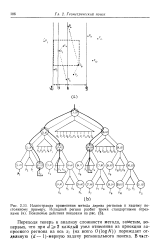 |
Иллюстрация применения метода дерева регионов к нашему постоянному примеру. Исходный регион разбит тремя стандартными отрезками ( а. Поисковые действия показаны на ( Ь. [7] |
Переходя теперь к анализу сложности метода, заметим, во-первых, что при d 2 каждый узел отнесения из проекции запросного региона на ось х ( их всего О ( log Л /)) порождает отдельную ( d - 1) - мерную задачу регионального поиска. [8]
Данная теорема является мощным средством анализа асимптотической сложности рекурсивных алгоритмов, использующих метод декомпозиции, но, к сожалению, она не дает возможности получить в явном виде коэффициенты функции трудоемкости. Для решения этой задачи необходим более детальный анализ рекурсивного дерева. [9]
Важным моментом второго этапа математического обеспечения является анализ сложности реализации алгоритма. [10]
Напомним, что здесь, как и в других местах, весь анализ сложности ( веса) основан на равномерной весовой функции. Если брать логарифмическую весовую функцию, то на анализе временной сложности может сказаться длина стека, используемого для реализации процедур с рекурсией. [11]
Другие применения абстрактной интерпретации состоят в изменении на месте структур данных, анализе сложности и анализе высказываний. [12]
Недостатки среднего тарифного разряда рабочих как сводной характеристики их квалификации необходимо учитывать в анализе сложности труда. Прежде всего средний тарифный разряд должен дополняться другими показателями, совместное рассмотрение которых позволит уточнить выводы о квалификации рабочих. [13]
Эта причина представляется наиболее существенной, поскольку она вызвана переходом от анализа качества к анализу сложности и связана с самой природой сложностных оценок. Она в одинаковой степени относится к вероятностным и комбинаторным оценкам, основанным на функции роста. [14]
Другие приложения, которые различаются главным образом по времени, необходимом для их создания, включают в себя анализ высказываний и анализ сложности. Первый связан с определением того, какое из рекурсивных уравнений в описаниях функции потребуется при данном вызове этой функции. Это важно в компьютерах с параллельной архитектурой, в которых может быть необходим удаленный доступ к разделяемым кодам. Путем определения того, какие части этого кода необходимы ( высказывания), можно значительно сократить количество сообщений, которые эти высказывания пересылают. Анализ сложности также важен для параллельных машин, особенно для машин с улучшенными структурными элементами. Если выражение содержит подвыражение, которое может быть вычислено независимо, например аргументы применения функции или выражение, значением которого является функция и которое применяется к выражению аргумента, то независимые вычисления могут быть поручены ( разбросаны) различным процессорам для параллельного выполнения. Однако такое распределение приводит к дальнейшему росту обмена информацией, и если стоимость разделения вычислений преобладает над выигрышем по времени выполнения вычислений, то смысла увеличивать степень параллелизма таким образом нет. Задача, поэтому, заключается в том, чтобы заранее, на этапе компиляции, знать, как долго будет происходить вычисление подвыражений. Возможно, что на это будет указывать некая мера сложности, определенная для выражений, и если они были выражены в терминах некой нестандартной семантики и домена, то абстрактная интерпретация может стать формальной основой для подобного анализа. [15]
Страницы: 1 2