Обратимость - чертеж
Cтраница 2
Заметим, что отмеченные нами свойства центральных проекций не обеспечивают однозначного соответствия оригинала, т.е. не обеспечивается обратимость чертежа. Это значит, что к использованному аппарату проецирования нужны дополнительные условия, позволяющие не только узнать точку по ее изображению, но и восстановить ее положение в пространстве. [16]
Параллельные проекции проще в построении изображений, обладают достаточно хорошей наглядностью, но решение геометрических задач в них все-таки затруднительно и, в представленном виде, они не обеспечивают обратимости чертежа. [17]
В 1.4 рассмотрен способ обеспечения обратимости чертежа проецированием на две взаимно перпендикулярные плоскости проекций, который повсеместно применяется в машиностроительном и строительном черчении. Обратимость чертежа обеспечивается и другими способами. [18]
Последние три требования не нуждаются в пояснениях. Раскроем понятие обратимости чертежа: чертеж называется обратимым, если по изображению фигуры можно восстановить ее форму, размеры и положение в пространстве. Очевидно, чертеж будет обратимым только в том случае, если между множествами геометрических фигур пространства и их изображений установлено взаимно однозначное соответствие. [19]
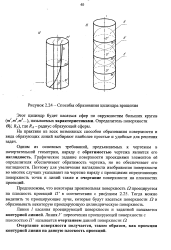 |
Способы образования цилиндра вращения. [20] |
Одним из основных требований, предъявляемых к чертежам в начертательной геометрии, наряду с обратимостью чертежа является его наглядность. Графическое задание поверхности проекциями элементов ее определителя обеспечивает обратимость чертежа, но не обеспечивает его наглядности. Поэтому для увеличения наглядности изображения поверхности во многих случаях указывают на чертеже наряду с проекциями определяющих поверхность точек и линий также и очертание поверхности на плоскостях проекций. [21]
Одним из основных требований, предъявляемых к чертежам в начертательной геометрии, наряду с обратимостью чертежа является его наглядность. Графическое задание поверхности проекциями элементов ее определителя обеспечивает обратимость чертежа, но не обеспечивает его наглядности. Поэтому для увеличения наглядности изображения поверхности во многих случаях указывают на чертеже наряду с проекциями определяющих поверхность точек и линий также и очертание поверхности на плоскостях проекций. [22]
Одним из основных требований, предъявляемых к чертежам в начертательной геометрии, наряду с обратимостью чертежа является его наглядность. Графическое задание поверхности проекциями элементов ее определителя обеспечивает обратимость чертежа, но не обеспечивает его наглядности. [23]
Что называют несобственными элементами пространства. Что называют обратимостью чертежа. [24]
Основным элементом чертежа является линия. Все поверхности оригинала необходимо задать на чертеже с помощью линий, поэтому фундаментальным классом задач, обеспечивающим процесс построения чертежа, являются задачи на построение общей части двух элементов. Именно взаимные пересечения элементов, инциденции обеспечивают обратимость чертежа, его полноту. Как известно, преобразование оригинала в изображение сопровождается потерей информации, поэтому множества Т и R дополняются не только правилами решения позиционных задач, но и правилами составления из элементов чертежа изображений, в которых будет сохранена необходимая информация. Фундаментальной задачей здесь являете задача геометрического измерения, а соответствующий класс задач, называемых метрическими, включает в себя отображение на чертеже перемещений оригинала в пространстве. Намеченные нами классы задач являются составными частями системы графического конструирования. В то же время каждый класс или процесс представляет собой иерархическую подсистему. [25]
 |
Образование аксонометрической проекции. [26] |
Основным недостатком комплексного чертежа является его низкая наглядность. Поэтому в инженерной практике, при необходимости, используют изображения, полученные способом параллельного проецирования на одну плоскость и называемые аксонометрическими проекциями. При этом дополнительным условием проецирования, обеспечивающим обратимость чертежа, служит прямоугольная система координат, которую называют натуральной. [27]
 |
Образование аксонометрической проекции. [28] |
Основным недостатком комплексного чертежа является его сравнительно низкая наглядность. Поэтому в инженерной практике, при необходимости, используют изображения, полученные проецированием на одну плоскость и называемые аксонометрическими проекциями. При этом дополнительным условием проецирования, обеспечивающим обратимость чертежа, служит прямоугольная система координат, которую называют натуральной. [29]
Страницы: 1 2