Анализ - последнее уравнение
Cтраница 1
Анализ последних уравнений показывает, что при прочих равных условиях частотные погрешности будут максимальны для коэффициентов преобразования, близких к 0 2 и 0 8, а при коэффициенте преобразования, равном 0 5, они будут минимальны. Это объясняется примерным равенством эквивалентных емкостей, нагружающих верхнюю и нижнюю части обмотки при йуном 0 5, и отличием этих емкостей при других коэффициентах преобразования. [1]
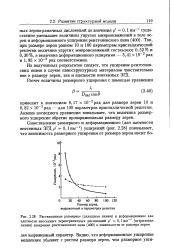
Анализ последнего уравнения показывает, что величина размерного уширения обратно пропорциональна размеру зерен. [3]
Анализ последних уравнений также приводит к выводу о том, что при номинальном нагружении ( dS 0, du 0) закритическая деформация осуществляется только при достаточной жесткости нагружающей системы, когда R RD, что согласуется с полученными ранее результатами. В противном случае происходит динамическое разрушение. Кроме того, равновесное деформирование при номинальном нагружении невозможно, если D ( e) 0, что соответствует ниспадающей ветви с отрицательной крутизной. [4]
Анализ последнего уравнения показывает, что если объем частиц V большой, то второй член очень мал и им можно пренебречь. И, наоборот, если при высокой степени дисперсности объем частиц V очень мал, энергия частиц будет в основном связана с энергией поверхности. Иными словами, в грубодисперсных системах преобладает объемная энергия, связанная с массой, а в высокодисперсных системах - поверхностная энергия. Дальнейшее дробление дисперсной фазы вплоть до молекул или ионов приводит к исчезновению поверхности раздела фаз. При этом второй член уравнения будет равен нулю. Так даже при малой концентрации, например 1 %, суммарная площадь поверхности раздела S в 1 л бентонитовой суспензии измеряется тысячами квадратных метров. [5]
Анализ последнего уравнения показывает пути повышения допустимого числа включений в час. Для этого необходимо увеличивать допустимые потери за счет применения двигателя с изоляцией повышенной теплостойкости и усиления вентиляции двигателя. [6]
Из анализа последнего уравнения следует, что логарифм величины, обратной сопротивлению реакции, ли нейно зависит от потенциала электрода. [7]
 |
Деформация абразивной ленты при набегании на поверхность ролика и ее натяжении под действием центробежных сил. [8] |
Из анализа последнего уравнения следует, что наибольшие напряжения от изгиба будут возникать при набегании ленты на ролики меньших диаметров. Напряжение от действия центробежных сил зависит от скорости вращения ленты, ее массы и угла охвата окружности ролика. [9]
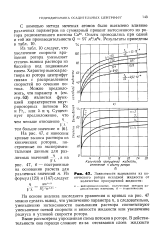 |
Зависимости вымывания из конического ротора исходной жидкости от количества пропущенной жидкости. [10] |
На основе анализа последнего уравнения и кривых на рис. 47 можно сделать вывод, что увеличению параметра п, а следовательно, уменьшению интенсивности вымывания раствора соответствуют уменьшение осевой скорости и вязкости жидкости или увеличение радиуса и угловой скорости ротора. [11]
Как видно из анализа последнего уравнения ( на это указывал и Сэвинс), трубка Пито не может быть использована для прямого измерения профиля скоростей в жидкостях, которым присущи явления нормальных напряжений. [12]
Страницы: 1