Анализ - форма - колебание
Cтраница 1
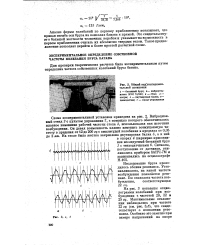 |
Общий вид эксперимея-тальной установки 1 - батанный бруе. 2 - виброустановка ВУС 70 / 200. 3 - стол. 4 - опоры. 5 - двутавровая балка. в - тенводатчик. 7 - пульт управления. [1] |
Анализ формы колебаний по первому приближению показывает, что кривая изгиба оси бруса на консолях близка к прямой. Это свидетельствует о большой жесткости челночных коробок и указывает на возможность в первом приближении считать их абсолютно твердым телом. Такое предпо дожение позволяет перейти к более простой расчетной схеме. [2]
Анализ форм колебаний и значений частных производных от частот по силовым параметрам для всех исследуемых молекул показывает, что частоты и формы колебаний являются характеристичными не для отдельных связей NF и углов FNF, а для всей группы NF2 в целом. [3]
Анализ форм колебаний, проведенный выше, приводит нас к тому пределу, который существует при использовании простых соображений симметрии. [4]
Анализ формы колебаний рамной конструкции фундамента показывает, что при любых скоростях вращения роторов, за исключением резонансных, точки верхней горизонтальной рамы колеблются в горизонтальных направлениях с различными амплитудами и в различных фазах. Поперечные рамы фундамента также колеблются со сдвигом фаз. Между колебаниями подшипников и элементов рам существует сдвиг фаз, изменяющийся с изменением числа оборотов роторов турбогенератора. [5]
Анализ формы колебаний фундамента рамной конструкции показывает, что при любых скоростях вращения роторов, за исключением резонансных, точки верхней горизонтальной рамы колеблются в горизонтальном направлении с различными амплитудами и в различных фазах. Поперечные рамы фундамента также колеблются со сдвигам фаз, изменяющимся в зависимости от числа оборотов турбогенератора. [6]
При анализе форм колебаний, соответствующих спектральным кривым разных семейств в окрестности частоты Q /, уже недостаточно следить только за рельефом плоских поверхностей диска. [7]
Это подтверждается анализом форм колебаний. [8]
Описанное выше явление краевого резонанса для тонкого диска так же четко проявляется и при анализе форм колебаний длинных цилиндров. При этом краевая мода характеризуется сильно выраженной локализацией области интенсивных движений вблизи торцов. Важно отметить, что в этом случае краевой резонанс в одинаковой мере проявляется как для симметричных, так и для антисимметричных относительно плоскости г 0 движений. [9]
 |
Нормированные формы колебаний линейных фрагментов N-С - Pt-С - N ( t oo / i Для типа Аи в координатах симметрии ( согласно. [10] |
Обычно частоты vx обозначают как v ( CN), хотя, как это следует из анализа форм колебаний, такое обозначение не строго и указывает лишь на связь, максимально изменяющуюся при колебании с данной частотой. Однако поскольку это обозначение общепринято, то мы в дальнейшем также будем пользоваться им, специально не оговаривая его условность. [11]
Динамические процессы в системе описываются известными дифференциальными уравнениями. Определим частоты собственных колебаний на основании анализа форм колебаний для симметричной системы. [12]
Таким образом, частота антисимметричных колебаний vuy зависит от массы всех атомов и постоянной квазиупругой силы. Это можно было предсказать вначале при анализе формы колебаний, так как в антисимметричных колебаниях принимают участие все три атома, а в симметричных - только крайние. [13]
По аналогии с относящимся к этому случаю рис. 85 на рис. 82 выделены участки спектральных кривых, которые можно объединить как относящиеся к бгмоде. Обоснование такого объединения указанных участков спектральных кривых следует из анализа форм колебаний на частотах, принадлежащих центрам этих плато. [14]
Спектр собственных частот на рис. 63 имеет характерные зоны, одна из которых выделена кривой S. Это обстоятельство необходимо иметь в виду, приступая к анализу форм колебаний. Формы колебаний, соответствующие определенному типу движений, проявляются только для частот, достаточно удаленных от зон взаимодействия. [15]
Страницы: 1 2