Окончание - удар
Cтраница 1
Окончание удара определяется условием равенства нулю полного напряжения 0 на ударяемом конце стержня. [2]
Это выражение дает распределение перемещений после окончания удара. [3]
Рассмотрим промежуточное состояние системы брусок-пуля непосредственно после окончания удара, когда пуля уже застряла в бруске, но нити еще занимают вертикальное положение. [4]
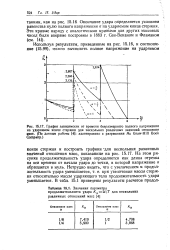
График деформаций в сечении х 0 позволяет уточнить время окончания удара. [5]
Момент, когда напряжение а обращается в нуль, указывает на окончание удара. [6]
При идеально упругом ударе все соударяющиеся тела восстанавливают свою форму после окончания удара. Это означает, что в состоянии этих тел не происходят какие-либо изменения, например, нет остаточных деформаций. [7]
Таким образом, здесь при ударе почти вся кинетическая энергия расходуется на деформацию соударяющихся тел; по окончании удара тела можно считать неподвижными. [8]
Таким образом, здесь при ударе почти вся кинетическая энергия расходуется на деформацию соударяющихся тел; но окончании удара тела можно считать неподвижными. [9]
Таким образом, здесь при ударе почти вся кинетическая энергия расходуется на деформацию соударяющихся тел; по окончании удара тела можно считать неподвижными. [10]
Следовательно, звено 1, которое до удара являлось ведущим ( в указанном выше смысле), к моменту окончания удара становится ведомым. [11]
 |
Схема взаимодействия сил при отскоке груза после удара о направляющую плоскость. [12] |
Второй этап - движение груза при отскоке после удара - протекает с начальными значениями кинематических параметров х и у, характеризующими движение груза в момент окончания удара. [13]
Пусть, как обычно, v - и v - векторы скоростей точек системы непосредственно до и после удара, a vv - вектор любой кинематически возможной скорости точки Pv в момент t - t о г окончания удара. [14]
Таким образом, найдена система четырех уравнений с неизвестными un, Win, N и Nz. Решая эту систему, получим исчерпывающий ответ на вопрос о движении точки после окончания удара. [15]
Страницы: 1 2