Оператор - шум
Cтраница 1
Оператор шума, имеющий подходящие корреляционные свойства, помогает сохранить коммутационное соотношение (9.1.10) в любой момент времени. Наличие в уравнении (9.1.15) шумового члена вместе с релаксационным членом является проявлением флуктуационно-диссипационной теоремы статистической механики, то есть диссипация всегда сопровождается флуктуациями. [1]
Эта 5-корреляция операторов шума является результатом предположения, что временная эволюция атома происходит намного быстрее эволюции поля излучения. [2]
Таким образом, оператор шума Fg не дает вклада в ширину линии излучения лазера. Это будет показано явно при строгом рассмотрении в следующих разделах. [3]
Интересно отметить, что присутствие оператора шума в уравнении (9.1.15) необходимо для сохранения коммутационного соотношения (9.1.10) в любой момент времени. [4]
Здесь § описывает затухание резонатора, F ( t) - оператор шума ( ср. [5]
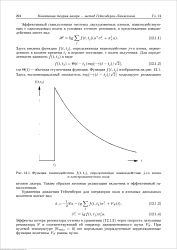 |
Функция взаимодействия f ( t tj, определяющая взаимодействие j - ro атома. [6] |
Эффекты потерь резонатора учтены в уравнении (12.1.3) через скорость затухания резонатора и соответствующий ей оператор ланжевеновского шума Fg. При нулевой температуре ( птепл 0) все нормально упорядоченные корреляционные функции величины Fg равны нулю. [7]
Таким образом, эволюция средних значений, содержащих оператор гармонического осциллятора, зависит от флуктуации резервуара. Оператор шума изменяется быстро, ибо содержит все частоты резервуара. [8]
Мы также представим подход квантовых скачков к теории релаксации. В следующих главах релаксация системы будет рассмотрена с привлечением метода оператора шума в представлении Гейзенберга. [9]
Эти корреляционные функции будут использоваться при выводе уравнений движения для корреляционных функций поля в разд. Далее мы рассмотрим затухание одномодового поля, взаимодействующего с атомным резервуаром, а также расширим и усилим данное рассмотрение резервуара осцилляторов. Главным результатом этого будет корреляционная функция оператора шума, которая не является дельта-функцией и, следовательно, соответствует окрашенному шуму, а не белому шуму, рассмотренному в этом разделе. [10]
Ширина линии излучения лазера является важной величиной. Например, она определяет фундаментальный предел работы активного кольцевого лазерного гироскопа. Первый полностью квантовый вывод выражения для спектральной ширины лазера был сделан методом оператора квантового шума 1) и был настолько общим, что включал в себя даже проблему ширины линии излучения полупроводникового лазера. Этот вывод излагается в гл. [11]
Страницы: 1