Определение - напряжение - изгиб
Cтраница 1
Определение напряжений изгиба в зубьях червячного колеса из-за переменной формы зубьев по их длине, искривленного основания зуба и наклонного положения контактной линии весьма сложно, вследствие чего оно осуществляется пока приближенным способом. Для этой цели используется зависимость для расчета косозубых цилиндрических колес, дающая после внесения в нее соответствующих коррективов удовлетворительную для практики точность. [1]
Для определения напряжения изгиба кулачковый вал рассматриваем как разрезную балку с опорами посередине его подшипников. [2]
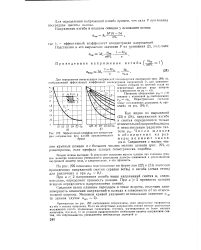 |
Эффективный коэффициент концентрации напряжения при изгибе призматического бруса. [3] |
Для определения напряжений изгиба примем, что сила Р приложена посередине высоты шлица. [4]
При определении напряжений изгиба предполагается, ято сила сосредоточена на краю опорной полки. Ребра, подкрепляющие полку, должны быть учтены при расчете. [5]
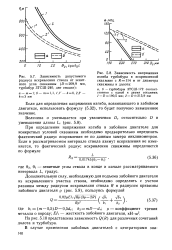
При определении напряжений изгиба и динамических напряжений в качестве расчетного параметра используется модуль продольной упругости материала Е, который, как отмечалось выше, также зависит от температурных условий эксплуатации. На рис. 36 приведены обобщенные данные о температурном изменении этой упругой характеристики для СБТ, ТБТ и ЛБТ. Обращает на себя внимание, что в отличие от предела текучести темп падения модуля продольной упругости для алюминиевых сплавов заметно ниже, чем для сталей и титановых сплавов. [6]
При определении напряжений изгиба и величины прогиба следует учесть общую жесткость стального ролика и намотанного рулона полотна или ткани. [7]
При определении напряжения изгиба в забойном двигателе для конкретных условий скважины необходимо предварительно определить фактический радиус искривления ее по данным замера инклинометром. [8]
При определении напряжения изгиба в забойном двигателе для конкретных условий скважины необходимо предварительно определить фактический радиус искривления ее по данным замера инклинометром. [10]
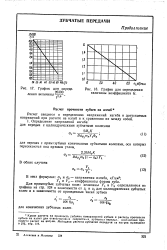 |
График для опреде.| График для определения величины коэффициента G. [11] |
Расчет сводится к определению напряжений изгиба и допускаемых напряжений при расчете на изгиб и к сравнению их между собой. [12]
При расчете приварного фланца производим определение напряжения изгиба, возникающего во фланце, и напряжения в сварных швах. [13]
Это расхождение несущественно отразится на определении напряжений изгиба, ввиду того, что изгибающие моменты имеют максимальное значение в центре пластины, а не на наружном контуре. Так как примененный метод приближенного решения позволяет получить решение в виде рядов, сходимость которых можно улучшить, его следует использовать для приближенной оценки влияния теплового растяжения на тепловой изгиб. [14]
Формула (2.81) может быть рекомендована для определения напряжений изгиба в поперечных сечениях колонны. [15]
Страницы: 1 2