Определение - тепловое напряжение
Cтраница 1
Определение тепловых напряжений и перемещений в теле непосредственным интегрированием соответствующих дифференциальных уравнений при произвольных граничных условиях является сложной задачей. Поэтому большой интерес представляют вариационные принципы термоупругости ( § 2.4), с помощью которых могут быть разработаны приближенные методы решения задач термоупругости, аналогичные известным вариационным методам решения задач изотермической теории упругости [34]: методы, основанные на обобщенном на случай задачи термоупругости вариационном уравнении Лагранжа и выражениях, аппроксимирующих возможные перемещения, и методы, основанные на обобщенном на случай задачи термоупругости принципе минимума энергии деформации и выражениях, аппроксимирующих возможные напряжения. [1]
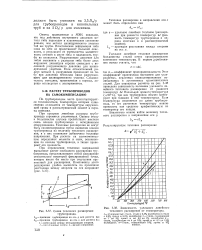 |
Схема теплового расширения. [2] |
При определении тепловых напряжений выполняют расчет свободного расширения трубопровода, представляющего собой расширение относительно некоторой фиксированной точки, которое имело бы место при отсутствии препятствий для расширения. [3]
При определении теплового напряжения топки д-у объем, зажимаемый ширмами, расположенными в верхней ее части и в районе выходного окна, включается в объем топки в том случае, если шаг ширм Si 700 мм. [4]
Во многих случаях для определения тепловых напряжений эффективно применение вариационных методов. [5]
Применение полученных решений иллюстрируется примерами определения тепловых напряжений в длинном сплошном цилиндре при конвективном теплообмене между его поверхностью и средой и воздействии линейного источника тепла, расположенного на оси цилиндра. [6]
В качестве примеров, иллюстрирующих применение методов решения плоских задач термоупругости, рассматривается определение тепловых напряжений в диске и цилиндре при плоском осесимметричном ( стационарном и нестационарном) температурном поле и при плоском неосесимметричном стационарном температурном поле. [7]
В качестве примеров, иллюстрирующих применение общего решения (6.1.1), в настоящей главе рассматривается определение тепловых напряжений в цилиндре конечной длины ( § 6.2) и в полой сфере ( § 6.3) при заданных температурных полях. [8]
Таким образом, метод решения задачи термоупругости, основанный на теореме взаимности работ, заключается в том, что определение тепловых напряжений, деформаций и перемещений сводится к задаче изотермической теории упругости о напряженном состоянии упругого тела под действием единичной сосредоточенной силы. [9]
В связи с указанным установилось мнение, что при исследовании термонапряженности конструкций учет динамических напряжении, вообще говоря, практического значения не имеет и для определения тепловых напряжений в условиях нестационарного теплообмена возможно применение квазистатических решений. Тем не менее исследования динамических задач термоупругости нуждаются в дальнейшем развитии в связи с условиями работы новых конструкций, подвергающихся действию импульсивных теплопотоков; здесь важным является также изучение условий возникновения и распространения в конструкциях термоупругих волн напряжений. [10]
Износ и разрушение материала при трении обусловлены совместным действием поверхностной температуры и температурного градиента, вызывающего напряжение в материале. Когда в материале возникает температурный градиент или когда материал, состоящий из двух и более веществ с различными коэффициентами расширения, нагревается, отдельные его волокна расширяются различно в соответствии с их температурой и коэффициентом расширения. Сопротивление материала тепловому импульсу понимается как стойкость материала в условиях мгновенной генерации тепла. Таким образом, проблема сопротивления тепловому импульсу и тепловым напряжениям сводится к определению тепловых напряжений, обусловленных температурным полем материала. [11]
Страницы: 1