Определение - пара
Cтраница 1
Определение пары также остается без изменения. [1]
Определение пары сил как бесконечно малой силы в бесконечно удаленной точке плоскости имеет в некоторых случаях известные преимущества. [2]
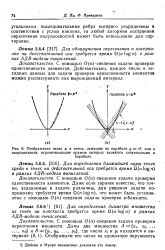 |
Отображения чисел / в точки, лежащие на параболе у х2, или в полуплоскости, ограничивающие прямые которых являются касательными к. [3] |
Для определения ближайшей пары точек среди п точек на действительной оси требуется время Q ( nlogra) в рамках АДВ-модели вычислений. [4]
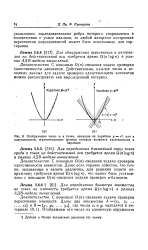 |
Отображения чисел х / в точки, лежащие на параболе у х2, или в полуплоскости, ограничивающие прямые которых являются касательными к. [5] |
Для определения ближайшей пары точек среди п точек на действительной оси требуется время Q ( nlogn) в рамках АДВ-модели вычислений. [6]
По определению пары, принадлежащие одному и тому же классу, называются равными и считается, что каждая такая пара определяет класс А. В множестве, элементами которого будут классы равных пар, определим операции сложения и умножения по следующим правилам. [7]
По определению пары, принадлежащие одному и тому же классу, называются равными и считается, что каждая такая пара определяет класс а. В множестве, элементами которого будут классы разных пар, определим операции сложения и умножения по следующим правилам. [8]
При всяком способе определения расслояемой пары условие рассло-яемости двух систем плоских элементов дает систему из шести уравнений на величины, определяющие лучи конгруэнции пары, причем эти шесть уравнений сводятся к пяти независимым. Первая особенность поставленной задачи в том, что одно из этих уравнений-конечное и допускает простое геометрическое истолкование. Будем называть расстояние между центром луча г и серединой отрезка, отсекаемого на луче г лучами гг, гг конгруэнции пары, эксцентриситетом пары, а угол между биссектрисой угла со сторонами, параллельными лучам гг, г2 пары, и вершиной, например, в центре луча г и биссекторомугла между фокальными плоскостями - асимметрией пары. В этих условиях теорема формулируется так: отношение двойного эксцентриситета пары, к синусу двойной асимметрии равно отношению расстояния между граничными точками общего перпендикуляра соответствующих лучей пары к косинусу угла между ними. Вторая особенность новой постановки задачи в том, что приведение системы из шести уравнений к пяти независимым не совершается единообразно во всех случаях. Многообразие этих особых пар зависит от четырех произвольных функций одного аргумента. Симметричные пары наиболее интересны. В отличие от особых пар симметричные пары общего типа всегда приводят к конфигурации Бахвалова. [9]
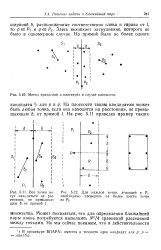 |
Метод разделяй и властвуй в случае плоскости.| Все точки мо - [ IMAGE ] Для каждой точки, лежащей в Р. [10] |
Может показаться, что для определения ближайшей пары вновь потребуется выполнить N2 / 4 сравнений расстояний между точками. [11]
В алгоритме Литтла правилом ветвления служит способ определения пары ( / с, Z), по которой производится разбиение. [12]
Для получения информации второго и третьего типа обычно можно ограничиться определением пары значений Mq, например М и Мш, комбинируя осмометрию и рассеяние с ета, или М и Мг по данным седиментационного равновесия. [13]
Нам хотелось бы рассмотреть несколько более детально, какие следствия вытекают из определения пары преобразований Фурье и в чем заключается их смысл. В частности, будет показано, что высокие пространственные частоты соответствуют резким изменениям интенсивности на изображении. [14]
Вторая часть предложения вытекает из следствия 3.9 и замечания, сделанного после определения ядерной пары. [15]
Страницы: 1 2