Определение - реакция
Cтраница 3
Для определения реакции в паре О нужно рассмотреть условия равновесия звена /, отделенного от стойки ( фиг. [31]
Для определения реакции Настюкова в пробирку диаметром 10 мм наливают 1 мл серной кислоты по ГОСТ 4204 - 66 и добавляют 3 капли испытуемого масла и 3 капли 40 % - ного раствора формальдегида. Смесь встряхивают в течение 5 сек. [32]
Для определения реакции в пробирку заливают 1 - 2 мл деэмулъгатора, небольшое количество нейтрализованного спирта, и все это разбавляют дистиллированной водой. Прибавлением нескольких капель фенолфталеина и метилоранжа фиксируют присутствие свободной щелочи или кислоты либо нейтральность. [33]
Для определения реакций в опорах Л и В рассмотрим равновесие балки АВ. В числе активных сил, приложенных к балке, имеется нагрузка, распределенная треугольником. Это - система непрерывно распределенных параллельных сил, направленных вертикально вниз и изменяющихся по модулю по линейному закону от до 2 кН / м до нуля. Заменим эту непрерывную нагрузку одной сосредоточенной силой - равнодействующей Q. Модуль силы Q равен площади треугольника. [34]
Для определения реакции и момента в заДблКе рассмотрим равновесие балки. [35]
Для определения реакций в точках А, В, О рассмотрим равновесие стержня СО. На стержень действует одна активная сила - сила тяжести Р, направленная по стержню. Стержень находится в равновесии под действием четырех сил: веса Р, реакций наклонной плоскости и цилиндрических шарниров А и В. [36]
Для определения реакции какой-либо связи отбрасывают эту связь и заменяют ее соответствующей реакцией, которую включают в число активных сил. [37]
Для определения реакций в стадии упругой деформации стержня необходимо составить уравнение деформации. [38]
Для определения реакций в кинематических парах рассматриваемого механизма в дополнение к уравнениям равновесия необходимо записать два независимых уравнения, пользуясь теорией упругости, потому что с точки зрения статики система остается дважды статически неопределимой. [39]
Для определения реакций в кинематических парах рассматриваемого механизма, в дополнение к уравнениям равновесия, необходимо записать два независимых уравнения, пользуясь теорией упругости, потому что с точки зрения статики система остается дважды статически неопределимой. [40]
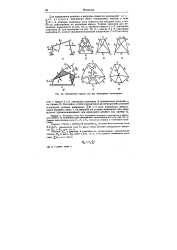 |
Построение планов сил для шарнирных механизмов. [41] |
Для определения реакции в шарнире совместно. Решение возможно, если известны все внешние силы и моменты, действующие на указанные звенья. [42]
 |
К определению.| Реакция приведенной непрерывной части системы ( б на смещенный во времени мгновенный импульс ( а. [43] |
Для определения реакции на последовательность импульсов необходимо сначала определить реакцию на один импульс. [44]
Для определения реакций в шарнире О применим следствие из принципа Даламбера для стержня с грузом, составив условия равновесия приложенных к ним внешних сил вместе с силой инерции груза. [45]
Страницы: 1 2 3 4