Статистическое определение

Cтраница 1

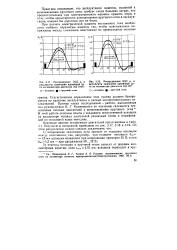Распределение ЭДС ес и результаты зажигания единичной дуги на коллекторе двигателя ЭД-104А.| Распределение ЭДС ек и результаты зажигания единичной дуги на коллекторе двигателя ЭД-107. [1]

Статистическое определение этих границ должно базироваться на практике эксплуатации и данных экспериментальных исследований. В этой работе описаны опыты с созданием искусственной вспышки на коллекторе тяговых двигателей различных типов и модификаций по описанной выше методике. [2]

Статистическое определение РСм ДЛЯ действующих предприятий осложняется трудностью выбор-а наиболее загруженной смены ( перенос начала работы разных категорий работников в пределах смены, четырехсменная работа и др.), сложения значений РСм для тех смен, которые не совпадают во времени. Имеет также место неопределенность производимых в системе электроснабжения измерений, особенно при их наложении на административно-территориальную структуру - потребления электроэнергии. Ограничения со стороны энергосистемы ведут к режимам, когда максимум нагрузки Рм встречается в одной смене, в то время как расход электроэнергии больше в другой. При определении Рр нужно отказаться от РСМ исключив промежуточные расчеты. [3]

Статистическое определение динамических характеристик связано с решением интегральных уравнений с ядром типа свертки, связывающих корреляционные функции случайно изменяющихся параметров с импульсной переходной функцией канала. Для разветвленного объекта, состоящего из нескольких последовательно соединенных недетектирующих звеньев, с многими входными величинами, каким является тепловая часть упрощенной структурной схемы ВУ, возникает практически неразрешимая задача решения сложной системы интегральных уравнений. Данная трудность может быть преодолена путем применения некоторых приближенных методов статистического определения динамических характеристик, резко сокращающих систему интегральных уравнений и, кроме того, не требующих их прямого решения. [4]

Статистическое определение энтропии равновесной системы (11.26) позволяет найти эту величину как функцию переменных Е, V, NI... [5]

Для статистического определения величины kr используются значения, Т 0н Т1, причем величина Т0 для аппаратуры однократного применения определяется по тем отказам, которые обнаруживаются на этапах хранения, профилактических работ и подготовки аппаратуры. [6]

Для статистического определения коэффициента корреляции между двумя случайными величинами i ] и 8 необходимо иметь ряд наблюдений этих величин. [7]

Для статистического определения коэффициента корреляции между двумя случайными величинами rt и & необходимо иметь ряд наблюдений за соответствующими значениями этих величин. [8]

Введенные выше классическое и статистическое определения понятия вероятности не являются достаточными для построения общей теории. [9]

По статистическому определению энтропия имеет максимум в равновесном состоянии, а это значит, что в любом неравновесном состоянии энтропия меньше, чем в равновесном. Поскольку замкнутая система самопроизвольно, в силу теплового движения, приходит к равновесному состоянию, энтропия неравновесных систем увеличивается. Это утверждение называется законом возрастания энтропии. [10]

При статистическом определении в качестве вероятности события принимают его относительную частоту. [11]

При статистическом определении в качестве вероятности события принимают его относительную частоту. [12]

При статистическом определении энтропии второй закон утрачивает абсолютный характер и превращается в статистический закон: за каким-либо заданным состоянием замкнутой системы будут следовать состояния, более вероятные если не с необходимостью, то в подавляющем большинстве случаев. [13]

Это несколько сложное статистическое определение параметра кооперативное б отражает основной физический факт: предшествование витка повышает вероятность образования следующего витка; виток как бы играет роль матрицы, облегчающей присоединение следующих звеньев в аналогичной конфигурации. С этим связан выигрыш свободной энергии - RT п а. [14]

В статье Новое статистическое определение энтропии ( 1925) содержится общая формулировка статистического выражения Больцмана и Гиббса энтропии S klogP для квантовых систем; Планк определяет Р как число стационарных состояний, энергия которых не должна превышать данного значения Е ( вместо того, чтобы взять сумму по всем состояниям в данном узком энергетическом интервале), и показывает, что это приводит к правильному выражению для системы осцилляторов и для одноатомного газа. [15]

Страницы: 1 2 3 4