Бит - перенос
Cтраница 2
Сложить старшие 4 бита ( старшее слово) и бит переноса, если он равен единице. [16]
Такое определение требует, чтобы ассемблер удерживал последнюю команду обновления бита переноса как команду обновления бита переноса с наивысшим приоритетом после процесса перераспределения. [17]
Если программный запрос выполнен нормально, то монитор записывает нуль в бит переноса. [18]
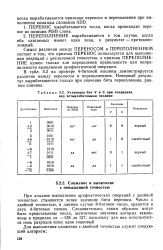 |
Установка бит V и С при операциях над четырехбитовыми числами. [19] |
При анализе выполнения арифметических операций с двойной точностью становится яснее значение бита переноса. Число с двойной точностью, в данном случае 8-битовое число, хранится в двух 4-битовых словах. Следовательно, таким образом могут быть представлены числа, десятичные значения которых заключены в пределах от - 128 до 127, поскольку для них используются семь разрядов плюс один знаковый. [20]
Из таблицы можно видеть, что при выполнении операции двоичного сложения может генерироваться бит переноса для использования на последующих этапах сложения. Полный сумматор имеет три входа для ввода второго слагаемого, первого слагаемого и бита переноса и два выхода, на которые выводится сумма и бит переноса. Если требуется складывать двоичные слова длиной два и более бит, то можно использовать последовательное соединение таких сумматоров, причем для двух соседних сумматоров выход переноса одного сумматора является входом для другого. На выходе этого сумматора генерируются трехразрядное слово ( DoDiD2) и бит переноса. [21]
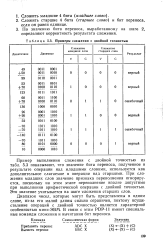 |
Примеры сложения с двойной точностью. [22] |
Пример выполнения сложения с двойной точностью из табл. 5.3 показывают, что значение бита переноса, полученное в результате операции над младшими словами, используется как дополнительное слагаемое в операции над старшими. При сложении младших слов значение признака переполнения игнорируется, поскольку на этом этапе переполнение вполне допустимо при выполнении арифметической операции с двойной точностью. Это значение учитывается на шаге сложения старших слов. [23]
Если разность - число положительное ( бит старшего разряда равен 0), то бит переноса необходимо отбросить; полученная последовательность битов и есть двоичный код результата. Если разность - число отрицательное ( бит старшего разряда равен 1), то она представлена в дополнительном коде. Выше указывалось, что для определения абсолютной величины отрицательного числа, представленного в таком виде, необходимо применить к нему операцию вычисления дополнительного кода. [24]
При выполнении арифметических операций с повышенной ( например, удвоенной) точностью необходимо, чтобы бит переноса ( или заема) передавался от младших слов или цифр к старшим. [25]
Правило, применяемое в случае сложения двоичных дополнительных чисел, гласит, что, если бит переноса в знаковый разряд совпадает с битом переноса из знакового разряда, бит переполнения можно игнорировать без риска вызвать ошибку; если же бит переноса в знаковый бит отличается от бита переполнения, результат неверный. [26]
Такое определение требует, чтобы ассемблер удерживал последнюю команду обновления бита переноса как команду обновления бита переноса с наивысшим приоритетом после процесса перераспределения. [27]
Логическая структура полусумматора такова, что состояние выхода S отображает бит суммы, а выхода Р - бит переноса. Это следует и из таблицы истинности полусумматора. [28]
Буквы г и / указывают на направление переноса символа, индексы при этих буквах - на переносимый символ ( влево машина носит бит переноса в следующий разряд, а вправо - добавляемый бит), в состоянии d машина осуществляет стирание обработанного разряда. [29]
Правило, применяемое в случае сложения двоичных дополнительных чисел, гласит, что, если бит переноса в знаковый разряд совпадает с битом переноса из знакового разряда, бит переполнения можно игнорировать без риска вызвать ошибку; если же бит переноса в знаковый бит отличается от бита переполнения, результат неверный. [30]
Страницы: 1 2 3 4