Общее определение

Cтраница 1

Общие определения даны для удобства комментариев и некоторых отступлений. [1]

Общее определение vm дано в формуле (3.406); более удобные для вычислений формулы будут выведены в гл. [2]

Общие определения и понятия котлов и их элементов. [3]

Общие определения, относящиеся к конусности, углу конуса, углу уклона и базорасстоянию, см. гл. К специфическим определениям, связанным с конической резьбой, относятся следующие. [4]

Общие определения и соотношения, выведенные в предыдущих параграфах для декартовых прямоугольных координат, могут быть выражены в цилиндрических координатах / -, 6, z посредством обычных формул преобразования координат. [5]

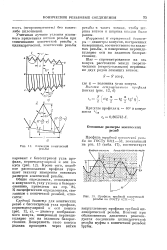Элементы конической резьбы.| Профиль трубной конической резьбы по ГОСТу 6211 - 52. [6]

Общие определения, относящиеся к конусности, углу уклона и базорас-стоянию, приведены на стр. [7]

Общие определения и соотношения, выведенные в предыдущих параграфах для декартовых прямоугольных координат, могут быть выражены в цилиндрических координатах г, 0, z посредством обычных формул преобразования координат. [8]

Общие определения и понятия котлов и их элементов. [9]

Общие определения, где указывается, в какую задачу и в какой комплекс задач входит данная программа, для какого варианта ЭВМ Искра написана программа и на каких ЭВМ она может выполняться, в какой системе выполнено написание программы, является ли система стандартной. [10]

Общее определение такого разделения состоит в следующем. [11]

Общее определение для двух видов пучков окружностей. Каждая точка прямой Оу, геометрического места центров окружностей ( С), составляющих пучок Г, имеет одну и ту же степень относительно всех окружностей ( С), равную квадрату радиуса той окружности ( С), центр которой лежит в этой точке. Если точка находится вне отрезка SH, то эта степень равна квадрату радиуса той окружности ( С), центром которой является эта точка. [12]

Общее определение интерполирующего и сглаживающего сплайнов. Пусть X, У - два гильбертовых пространства, Т: X - - - - У - линейный ограниченный оператор, действующий из X в Y. [13]

Последовательные приближения ковра Серпинского. [14]

Общее определение линии на плоскости было дано Кантором в 70 - е годы XIX века. [15]

Страницы: 1 2 3 4