Определитель - четвертый порядок
Cтраница 2
Згу методику можно применить и далее, заменив расчет определителя пятого порядка расчетом определителя четвертого порядка и проверкой еще одного практического критерия. [16]
Коэффициент, получающийся при х и строящийся из определителей третьего порядка по образцу ( 8), мы назовем определителем четвертого порядка. [17]
Коэффициент, получающийся при zi и строящийся из определителей третьего порядка по образцу ( 8), мы назовем определителем четвертого порядка. [18]
Выбор того или иного выражения практического критерия в каж-цом конкретном случае осуществляется исходя из условия максимально возможного сокращения объема расчетов и в значительной степени определяется видом схемы исследуемой системы. Это означает, что расчет определителя четвертого порядка ( УИ4): водится к более простому расчету произведения двух определителей второго порядка. Рациональный выбор практических критериев в общем случае может значительно облегчить анализ статической устойчивости по сравнению с непосредственным вычислением свободного злена характеристического уравнения. [19]
Тогда все определители шестого порядка, составленные из элементов матрицы (23.5), должны равняться нулю. Можно утверждать, что среди определителей четвертого порядка, составленных из первых шести столбцов, найдется по крайней мере один, отличный от нуля, так как в противном случае Т1 было бы плоским. [20]
Определителями первой матрицы являются координаты точки; они не требуют дальнейших исследований. Четвертая матрица уже сама является определителем четвертого порядка и дает, как известно, ушестеренный объем тетраэдра ( 1, 2, 3, 4), который можно, в соответствии с вводимыми в дальнейшем терминами, назвать пространственным элементом. [21]
Все свойства определителей, перечисленные в § 4, относятся к определителям любого порядка. В настоящем лараграфе следует применить эти свойства для вычисления определителей четвертого порядка. [22]
Все свойства определителей, перечисленные в § 4, относятся к определителям любого порядка. В настоящем параграфе следует применить эти свойства для вычисления определителей четвертого порядка. [23]
Учитывая, что при смещении узлов пояса в противоположные стороны в местах примыкания поперечных раскосов эпюра изгибающих моментов пересекает ось пояса, вводим здесь шарниры. Таким образом, задача устойчивости при симметричной форме искривления сводится к раскрытию определителя четвертого порядка. [24]
Учитывая, что при смещении узлов пояса во взаимно противоположные стороны эпюра моментов пересекает ось пояса, в узлах примыкания поперечных раскосов вводим шарниры. Таким образом, задача устойчивости при симметричной форме искривления сводится к раскрытию определителя четвертого порядка. [25]
В этом случае, как показывает фиг. Преимущества метода моментов перед методом Граммеля в данном случае реализуется в том, что для расчета первых четырех частот можно использовать определитель четвертого порядка, а не восьмого. [26]
При этом сумма берется по всевозможным перестановкам. Знак перед каждым членом определителя в разложении (3.105) определяется числом е инверсий ( беспорядков) в соответствующей перестановке. Например, член 13 21 34 42 в определителе четвертого порядка должен быть со знаком минус, так как перестановка ( 3, 1, 4, 2) имеет три инверсии. [27]
Формулы (5.2) являются центральными для производных. Он удобен тем, что в нем при любой величине шага сетки решение сводится к раскрытию определителя четвертого порядка. Это позволяет, уменьшая последовательно шаг, получить точный результат. [28]
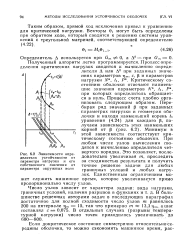 |
Зависимости определителя устойчивости от параметра нагрузки и его собственного значения от параметра окружных волн. [29] |
Критическому состоянию оболочки отвечают наименьшие значения параметров N, t, P, при которых определитель обращается в нуль. Процесс счета удобно организовать следующим образом. Минимум в этой зависимости соответствует критическому состоянию оболочки. При любом числе узлов вычисления сводятся к вычислению определителя четвертого порядка. Это позволяет последовательно увеличивая т, проследить за сходимостью результата и получить точное решение задачи для любых граничных условий и любых нагрузок. [30]
Страницы: 1 2