Частичный автомат

Cтраница 1

Частичным автоматом называется абстрактный автомат, у которого функция переходов или функция выходов ( обычная или сдвинутая), или обе эти функции, определены не для всех пар значений своих аргументов а их. [1]

Беря соответствующий частичный автомат, где эти переходы и выходы не определены вовсе, мы тем самым оставляем за собой право определить их впоследствии так, как это нам будет удобно. [2]

Для частичных автоматов употребляются те же способы задания, что и для вполне определенных автоматов. В тех местах таблицы переходов или таблицы выходов ( обычной или сдвинутой), в которых изображаемые ими функции не определены, мы будем ставить черточки. Граф частичного автомата чможет иметь вершины, из которых не выходят стрелки, обозначенные теми или иными входными сигналами. [3]

Для частичных автоматов Мура естественно считать запрещенными все состояния, для которых сдвинутая функция выходов не определена. Легко понять, что перейти из начального состояния в запрещенное под воздействием непустого слова автомат Мура может лишь в том случае, когда это слово - запрещенное. [4]

Для частичных автоматов Мили и Мура в рассмотренных таблицах на месте неопределенных состояний и выходных сигналов ставится прочерк. [5]

В случае частичных автоматов помимо эквивалентности и изоморфизма автоматов часто используются понятия эквивалентного и изоморфного продолжения автоматов. [6]

Сущность задачи минимизации частичных автоматов состоит в следующем: дан частичный автомат ( Мура или Мили) А, индуцирующий частичное автоматное отображение ф, определенное на некотором множестве М слов входного алфавита. Требуется построить частичный автомат ( Мура или соответственно Мили) В, который индуцирует частичное автоматное отображение, совпадающее на множестве М с отображением ф, и имеет наименьшее число внутренних состояний среди всех автоматов ( Мура или Мили), удовлетворяющих этому условию. [7]

В отличие от частичных автоматов, рассматривавшиеся ранее автоматы называются вполне определенными. [8]

Для случая же частичных автоматов свойство транзитивности для отношения / - совместимости, вообще говоря, не выполняется. [9]

В случае же частичных автоматов дело обстоит гораздо сложнее: с построением ос-классов и нормальной формы процесс минимизации, вообще говоря, не заканчивается. [10]

Если функцию переходов произвольного частичного автомата Мили А рассматривать не заданной во всех точках, в которых не задана его функция выходов то возникший таким образом новый частичный автомат Мили В будет, индуцировать то же самое частичное отображение, что и автомат А. [11]

Не изменяя индуцируемого частичным автоматом Мура частичного отображения, можно считать функцию переходов этого автомата неопределенной всякий раз, когда она принимает запрещенное значение. [12]

Подобно вполне определенным автоматам частичные автоматы также делятся на автоматы первого и второго рода, автоматы Мили и автоматы Мура. Изоморфизм частичных автоматов предусматривает, чтобы соответствующее изоморфное отображение переводило множества значений, в которых не определены функции переходов или выходов ( обычная или сдвинутая) одного автомата, в множества значений, в которых не определены соответствующие функции другого автомата. [13]

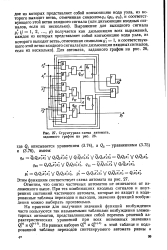Структурная схема автомата, заданного графом на 26. [14]

Отметим, что синтез частичных автоматов не отличается от изложенного выше. При тех комбинациях входных сигналов и внутренних состояний частичного автомата, которые не входят в кодированные таблицы переходов и выходов, значения функций возбуждения можно выбирать произвольно. [15]

Страницы: 1 2 3 4