Асинхронный автомат
Cтраница 2
В противоположность синхронным автоматам, в асинхронных автоматах моменты переходов из одного состояния в другое заранее не определены и могут совершаться через неравные между собой промежутки времени. Для асинхронных автоматов можно ввести дискретное время, определяемое исключительно лишь одними моментами фактических переходов автомата из одного состояния в другое. Однако при этом теория асинхронных автоматов становится существенно отличной от соответствующей теории для синхронного случая. Поэтому мы в качестве мо-ментов дискретного автоматного времени для асинхронных автоматов будем рассматривать не только моменты фактически имевших место переходов, но также и такие моменты, в которые переходы были возможны, но фактически не произошли. Разумеется, при этом необходимо считать, что интервал дискретности автомата ограничивает минимально возможное расстояние между лополнительно вводимыми моментами автоматного времени. [16]
При этом, как и ранее, состояние устройства в момент времени tn предполагается однозначно определяющимся по входному сигналу и состоянию устройства в момент времени tn, а выходные сигналы в моменты ta, rs i - TS J. Возникающая в результате модель представляет собой содержательную модель абстрактного конечного асинхронного автомата. [17]
В асинхронных автоматах длительность интервала времени Т - величина переменная, определяемая только моментами изменения состояния входа. При этом, обычно, принимается, что состояние входа асинхронного автомата может измениться лишь после того, как автомат перейдет в определенное внутреннее состояние. [18]
Такой процесс функционирования называется основным процессом. Граф переходов, построенный по табл. 4.11, показан на рис. 4.12. Отличительной особенностью графа переходов асинхронного автомата является наличие петель у каждой вершины графа. Первый переход по петле, означает, что достигнуто устойчивое состояние, соответствующее данной вершине графа. [19]
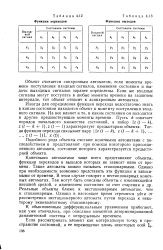 |
Функция переходов.| Функция выходов. [20] |
Объект считается синхронным автоматом, если моменты времени поступления входных сигналов, изменение состояния и выдачи выходных сигналов заранее определены. Если же входные сигналы могут поступать в любые моменты времени на заданном интервале, тот объект относят к асинхронным автоматам. [21]
Там, где задача раскраски усложнена дополнительными условиями одноцветности вершин, эффективным может оказаться и подход, предполагающий нахождение наибольшего пустого или полного подграфа, а затем группирование около вершин, вошедших в этот подграф, остальных вершин заданного графа. С помощью этого подхода, как показано в [26], можно решить такие задачи, как минимизация длины кода состояний асинхронного автомата, сжатие таблицы переходов автомата ( по строкам и столбцам), параллельная декомпозиция автомата, упрощение системы булевых функций, описывающих асинхронный автомат. Точно так же можно решать и все остальные задачи, перечисленные выше. Из рассмотренных здесь подходов к решению задач логического проектирования данный подход единственно пригоден для решения таких задач абстрактного синтеза автоматов, как минимизация числа состояний синхронного автомата и его декомпозиция. [22]
Различают два вида автоматов: синхронные и асинхронные. В синхронных автоматах переходы из одних состояний в другие осуществляются через равные временные промежутки, задаваемые обычно генератором тактовых импульсов, в то время как в асинхронных автоматах эти переходы совершаются через неравные между собой промежутки времени. [23]
К числу наиболее известных интерпретаций Р - задачи относятся ставшие классическими задачи о минимизации булевых функций в классе дизъюнктивных нормальных форм ( ДНФ) и о минимизации длины кода внутренних состояний асинхронного автомата. Проведенный в [10] анализ рассматриваемых в работе [21] оптимизационных задач проектирования дискретных устройств в базисе ПЛМ показал, что кроме упомянутых выше задач минимизации ДНФ булевых функций и минимизации длины кода внутренних состояний асинхронного автомата интерпретациями Р - задачи являются также разнообразные оптимизационные задачи, возникающие при синтезе одноярусных сетей из ПЛМ, минимизации секвенциальных автоматов, нахождении минимального дизъюнктивного базиса для заданного множества булевых векторов, построении проверяющего теста для транзисторной матрицы, реализующей систему элементарных конъюнкций, а также при построении диагностического теста для дизъюнктивной матричной схемы, если в ней возможны любые кратные неисправности типа исчезновения транзисторов. [24]
Там, где задача раскраски усложнена дополнительными условиями одноцветности вершин, эффективным может оказаться и подход, предполагающий нахождение наибольшего пустого или полного подграфа, а затем группирование около вершин, вошедших в этот подграф, остальных вершин заданного графа. С помощью этого подхода, как показано в [26], можно решить такие задачи, как минимизация длины кода состояний асинхронного автомата, сжатие таблицы переходов автомата ( по строкам и столбцам), параллельная декомпозиция автомата, упрощение системы булевых функций, описывающих асинхронный автомат. Точно так же можно решать и все остальные задачи, перечисленные выше. Из рассмотренных здесь подходов к решению задач логического проектирования данный подход единственно пригоден для решения таких задач абстрактного синтеза автоматов, как минимизация числа состояний синхронного автомата и его декомпозиция. [25]
Особенностью логических схем с обратными связями ( их определение приведено в § 3 - 6) является зависимость состояния выходов схемы не только от значений входных переменных в данном такте, но и от сигналов, действовавших в предыдущие моменты времени. Поэтому такая схема может рассматриваться как цифровой автомат. Различают синхронные и асинхронные автоматы. В синхронных автоматах переходы из одних состояний в другие осуществляются через равные промежутки времени, задаваемые генератором синхронизирующих сигналов. [26]
В противоположность синхронным автоматам, в асинхронных автоматах моменты переходов из одного состояния в другое заранее не определены и могут совершаться через неравные между собой промежутки времени. Для асинхронных автоматов можно ввести дискретное время, определяемое исключительно лишь одними моментами фактических переходов автомата из одного состояния в другое. Однако при этом теория асинхронных автоматов становится существенно отличной от соответствующей теории для синхронного случая. Поэтому мы в качестве мо-ментов дискретного автоматного времени для асинхронных автоматов будем рассматривать не только моменты фактически имевших место переходов, но также и такие моменты, в которые переходы были возможны, но фактически не произошли. Разумеется, при этом необходимо считать, что интервал дискретности автомата ограничивает минимально возможное расстояние между лополнительно вводимыми моментами автоматного времени. [27]
Автоматы, которые проектируются для работы без синхронизирующих тактовых импульсов, называются асинхронными. Они используются тогда, когда входные символы поступают на автомат в случайные моменты времени. Выполняя те же функции, асинхронные автоматы оказываются более быстродействующими, чем синхронные. В реальном автомате каждый элемент, входящий в его состав, вносит некоторую задержку или запаздывание, равное времени, которое должно пройти, чтобы изменение входной переменной элемента вызвало изменение его выходной переменной. [28]
В базис входит два типа электронных элементов: логические и запоминающие. Запоминающими элементами служат некоторые элементарные последовательностные автоматы. Триггер есть запоминающий синхронный или асинхронный автомат с двумя внутренними устойчивыми состояниями, каждое из которых может быть изменено под действием внешних входных сигналов. [29]
Автоматное отображение XS - S-Y задается, как правило, в виде графа переходов Gn S, ( U, ( X, У)), ( U S2), вершины которого взаимно однозначно соответствуют внутренним состояниям автомата, а дуги-переходам между ними, причем каждая дуга взвешена парой векторов ( X, У), при которой этот переход осуществляется. В целях упрощения задания автомата параллельные дуги графа переходов могут склеиваться. В этом случае некоторые компоненты входных и выходных векторов обозначаются символом -, указывающим на то, что при осуществлении данного перехода значение сигнала, приписанного данной компоненте вектора, несущественно для функционирования устройства. У асинхронного автомата каждая дуга графа переходов дублируется в концевой вершине петлей, взвешенной той же парой векторов ( X, Y), что и соответствующая дуга. Для графа переходов синхронного автомата это условие может не выполняться. [30]
Страницы: 1 2 3