Диагональный блок - матрица
Cтраница 1
Диагональные блоки матрицы А представляют собой одинаковые или разные квадратные матрицы ортонормированных фундаментальных функций, описывающих состояние стержней. [1]
Диагональные блоки матрицы А представляют собой одинаковые или разные квадратные матрицы ортонормированных фундаментальных функций, описывающих состояния стержней. [2]
Диагональные блоки матрицы А представляют собой одинаковые или разные квадратные матрицы ортонормированных фундаментальных функций, описывающих состояние стержней. [3]
В принадлежат одному и тому же диагональному блоку матрицы В. [4]
Структура матрицы D такова, что диагональному блоку матрицы U, который образован матрицей С, отвечает в D скалярная матрица, т.е. единичная матрица, умноженная на число Ка. D соответствующий блок U образован единичной матрицей. [5]
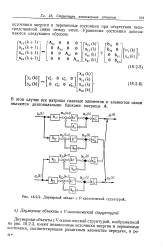 |
Двумерный объект с Р - канонической структурой. [6] |
В этом случае все матрицы главных элементов и элементов связи являются диагональными блоками матрицы А. [7]
Приводимое ниже следствие теоремы 3.5.1 можно применить для определения столбцов матрицы В, принадлежащих различным диагональным блокам матрицы В. [8]
Так как вершины графа QD, лежащие на одном и том же направленном цикле, принадлежат одному и тому же диагональному блоку матрицы В, то можно использовать матрицу F для оп - ределения матрицы В по полученной матрице В следующим образом. [9]
Ре 1 тогда и только тогда, когда 1-я и - я строки матрицы В принадлежат одному и тому же диагональному блоку матрицы В. [10]
Из теоремы 3.5.1 известно, что условие / р 1 означает, что i-я и р-я строки принадлежат одному и тому же диагональному блоку матрицы В, и поскольку / - и столбец имеет по крайней мере один ненулевой элемент в р-й строке, постольку / - и столбец должен находиться в том же диагональном блоке, что и 1-я и р-я строки. Таким образом, равенство f j 1 означает, ч то t - я строка и / - и столбец принадлежат одному и тому же диагональному блоку. Этим завершается доказательство следствия. [11]
Поэтому для всех h, таких, что 2ft v, матрица W2h остается той же и существует некоторое h, для которого формула (3.5.4) верна и e jW24 в ] 1 тогда и только тогда, когда 1-я и / - я строки матрицы В принадлежат одному и тому же диагональному блоку матрицы В. Этим завершается доказательство теоремы. [12]
Все объемные и поверхностные интегралы, необходимые при вычислении недиагональных блоков из уравнения (4.47), могут быть определены при помощи различных формул численного интегрирования, рассмотренных ранее ( см. разд. Диагональные блоки матрицы G, а в некоторых случаях ( как указано в предыдущем параграфе) и матрицы F должны определяться при помощи разбиения интегралов на две части, как показано в разд. Включающие постоянную часть базисной функции интегралы вычисляются с помощью введения локальной системы координат, показанной на рис. 4.6, с последующим ( описанным выше) преобразованием результатов к глобальной системе координат. [13]
Очевидно, что ftf e Fel 1 тогда и только тогда, когда j - я и / - я строки принадлежат одному и тому же диагональному блоку. Таким образом, все строки матрицы В, которые соответствуют ненулевым элементам первого столбца матрицы F, принадлежат первому диагональному блоку. Если все строки матрицы F, для которых / л 1, учтены, то следующий ненулевой столбец матрицы F может быть использован таким же образом, как и первый столбец этой матрицы, для нахождения строк матрицы В, принадлежащих второму диагональному блоку м-атрицы В и так далее. Таким путем можно найти диагональные блоки матрицы В, к которым принадлежит каждая строка матрицы В. [14]
В данной работе мы предлагаем метод проверки идентифицируемости, позволяющий несколько уменьшить сложность символьных выражений. Уравнения, полученные с помощью метода преобразования подобия, являются билинейными, мы же рассматриваем их как линейные относительно части неизвестных. На первом этапе матрица линейной системы уравнений перестановками строк и столбцов приводится к верхнему блочно-треугольному виду. Затем, применяя метод Гаусса отдельно к каждому диагональному блоку матрицы, на основании условия совместности системы линейных уравнений мы генерируем результирующие системы нелинейных уравнений, которые проверяем на разрешимость с помощью метода базисов Гребнера. [15]
Страницы: 1