Патч
Cтраница 1
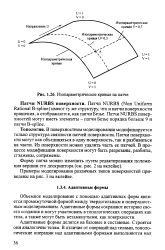 |
Изопараметрические кривые на патче. [1] |
Патчи NURBS ( Non Uniform Rational B-spline) имеют ту же структуру, что и патчи поверхности вращения, а отображаются, как патчи Безье. [2]
 |
B-spline и кривая Безье, построенные по одинаковым дескрипторам. [3] |
Ограниченный патч формируется тремя или четырьмя граничными кривыми. [4]
Патч поверхности вращения - это аналитически точный патч, поскольку для его построения используются образующая поверхности вращения, ось и угол поворота образующей ( так же как и для модели твердого тела), а не дескриптор. [5]
Положение точки на поверхности патча описывается параметрами U и V. [6]
Патч поверхности вращения - это аналитически точный патч, поскольку для его построения используются образующая поверхности вращения, ось и угол поворота образующей ( так же как и для модели твердого тела), а не дескриптор. [7]
Два понятия - топологическая поверхность и патч - являются основными понятиями поверхностного моделирования. [8]
Когда происходит размещение элемента библиотеки, патч просто вставляется в чертеж так, что он перекрывает все элементы. [9]
Эквидистантный патч поверхности строится по ранее созданному патчу на заданном расстоянии по нормалям в каждой точке. Эквидистантный патч не имеет своего дескриптора. [10]
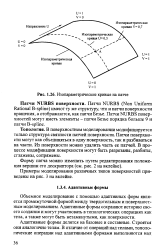 |
Изопараметрические кривые на патче. [11] |
Патчи NURBS ( Non Uniform Rational B-spline) имеют ту же структуру, что и патчи поверхности вращения, а отображаются, как патчи Безье. [12]
Существенное свойство мыла состоит в том, чтоб оное совершенно растворялось в воде, а патче в тончайшем винном спирте 2 ( Spir. [13]
Геометрическое место точек, принадлежащих кривой Безье в процессе ее перемещения вдоль другой кривой Безье, называется патчем поверхности Безье. Совокупность дескрипторов кривых Безье называется дескриптором патча Безье. Каждая точка на патче поверхности Безье совпадает с точкой пересечения изопараметрических кривых с заданными значениями параметров U и V. [14]
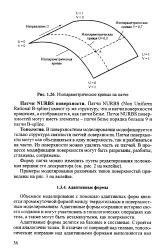 |
Изопараметрические кривые на патче. [15] |
Страницы: 1 2