Пекерис
Cтраница 1
Пекерис и др. [120] разработали модель геомагнитного динамо, построенную иа замкнутых вихревых кольцах, в которой диссипирует в десять раз меньше энергии, так как в этой модели нет азимутального поля. Буссе [23, 25] исследовал кои - Векцию, имеющую вид цилиндрических валиков, где общая неоднородность вращения отсутствует. [1]
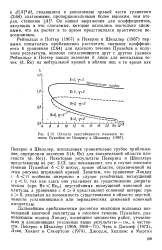 |
Области неустойчивости плоского те чения Пуазейля по Пекерису и Школлеру ( 1967. [2] |
Некоторые результаты Пекериса и Школлера представлены на рис. 2.13; они показывают, что в случае плоского течения Пуазейля б 0 всюду, кроме области, ограниченной на этом рисунке штриховой кривой. Заметим, что уравнение Ландау с б 0 особенно интересно в случае устойчивых возмущений с у 0, так как здесь оно указывает на существование докрити-ческих ( при Re Recr) неустойчивых возмущений конечной амплитуды, а уравнение с б О представляет основной интерес при Y 0, указывая на возможность существования в области неустойчивости установившихся или периодических движений конечной амплитуды. [3]
 |
Качественная динамика видимой кавитационной зоны ( h Зсм ( расчет. 1 - начальный радиус заряда. 2 - полость с продуктами детонации. 3 - кавитация. 4 - фронт волны разрежения. [4] |
Вторая точка зрения, высказанная Пекерисом, более обоснована. При экспериментах по взрыву глубинных бомб им установлено, что замедление роста купола втрое превышает ускорение силы тяжести. Возможны две причины: влияние воздушного сопротивления при распылении капель ( тогда купол - брызги) или действие внешнего избыточного давления на движущийся сплошной слой жидкости. Пекерисом показано [13.1], что при оценках по сплошному слою толщина откола должна составлять не менее 3 м, что маловероятно. [5]
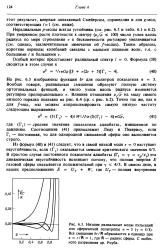 |
Низшие радиальные моды пульсаций для сферической политропы п 3 ( у 5 / 3. Все смещения бг / R обращаются в единицу при r / R 1, где R - радиус сферы. С любезного разрешения др. Роуба. [6] |
Соотношение ( 41) принадлежит Леду и Пекерису, если F. [7]
В отсутствие вращения эти / - моды, а также р - и g - моды, определяемые уравнением ( 61), очень похожи на моды, найденные Пекерисом для однородной сферы [ см. разд. [8]
Уравнение (6.10) действительно служит достаточно хорошим приближенным выражением для положения поверхности раздела при L c, например в случае замерзания воды. Второе приближение найдено Пекерисом и Слих-тером [29], которые воспользовались методом разложения в ряд. [9]
Уравнение (6.10) действительно служит достаточно хорошим приближенным выражением для положения поверхности раздела при L ct например в случае замерзания воды. Второе приближение найдено Пекерисом и Слих-тером [29], которые воспользовались методом разложения в ряд. [10]
 |
Волновые поверхности, образующиеся при распределенном вдоль линии ударном воздействии на анизотропное полупространство. [11] |
Обобщение этого решения на случай соударения с упругим телом к настоящему времени не получено. Волны, образующиеся при сосредоточенном ударном нагру-жении изотропного полупространства, изучались Пекерисом 11351, который показал, что большие поверхностные напряжения распространяются со скоростью поверхностных волн Релея. Однако решение динамической задачи об ударе упругой сферы по упругому полупространству до настоящего времени не известно. [12]
Ось х направлена вдоль волновода. Случай волновода с двумя акустически мягкими стенками, соответствующий модели Пекериса ( см. [ Толстой, Клей, 1969 ]), рассматривается аналогичным образом. Под углом 0 к оси волновода, совпадающей с осью х, излучается высоконаправленный бигармонический пучок накачки с частотами о. При достаточно малом затухании пучок накачки испытывает многократные отражения от границ волновода. [13]
Задача определения характеристических чисел, связанная с решением уравнения (3.11), была предметом исследования ряда авторов. К тому же выводу приходили и такие авторы как: Мизес, Хопф ( Hopf), Гольдштейн ( Goldstein), Пекерис ( Pekeris) и многие другие. Если не считать теории Гейзенберга3), которая считалась неполной и неточной и не была поэтому общепризнана, все теоретические работы до сравнительно недавнего времени давали отсутствие возможности потери устойчивости движения между двумя пластинками. В этой же работе дается попутно анализ ошибок, или неточностей, из-за которых ни один из предыдущих авторов не мог добиться верного результата. [14]
Задача определения характеристических чисел, связанная с решением уравнения (3.11), была предметом исследования ряда авторов. К тому же выводу приходили и такие авторы как: Мизес, Хопф ( Hopf), Гольдштейн ( Goldstein), Пекерис ( Pekeris) и многие другие. Если не считать теории Гейзенберга3), которая считалась неполной и неточной и не была поэтому общепризнана, все теоретические работы до сравнительно недавнего времени давали отсутствие возможности потери устойчивости движения между двумя пластинками. В этой же работе дается попутно анализ ошибок, или неточностей, из-за которых ни один из предыдущих авторов не мог добиться верного результата. [15]
Страницы: 1 2