Частичный перебор

Cтраница 2

Поэтому разыскание максимума / ( со) путем прямого перебора по всем со при сколько-нибудь больших п практически неосуществимо. Полный перебор вариантов здесь заменяется направленным частичным перебором, позволяющим отбрасывать большие группы вариантов, заведомо не дающих оптимума. [16]

В оценочных моделях пользуются также методами частичного перебора, не обеспечивающего, однако, попадания в глобальный минимум. [17]

В рассмотренной задаче структурного топологического синтеза, формулируемой как задача целочисленного математического программирования, перебор осуществляется на множестве малой мощности, что допускает даже полный перебор. Но большинство реальных задач структурного синтеза имеет гораздо большую размерность, поэтому при их решении допустим только частичный перебор. Так, количество просматриваемых вариантов L может оказаться экспоненциальной функцией размерности задачи п: L fee, где k - коэффициент пропорциональности. [18]

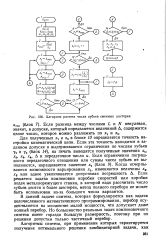Алгоритм расчета числа зубьев сменных шестерен. [19]

В данной задаче синтеза, которая формулируется как задача целочисленного математического программирования, перебор осуществляется на множестве малой мощности, что допускает даже полный перебор. Но большинство реальных задач компоновочного синтеза имеет гораздо большую размерность, поэтому при их решении допустим только частичный перебор. [20]

Дерево синтеза ХТС. [21]

Большое число возможных вариантов ( ветвей дерева) ограничивает применение комбинаторных методов. Поэтому для практического использования годятся только те из них, которые производят не полный, а частичный перебор вариантов. [22]

Поставленная задача (3.21) - (3.22) содержит непрерывные ( А /) и двоичные ( х /) переменные. В этом параграфе будет решена задача оптимизации только по непрерывным переменным; оптимизация по двоичным переменным осуществлена частичным перебором в следующем параграфе. [23]

Как следует из (3.1.1) - (3.1.7) и (3.1.8) - (3.1.15), общая задача синтеза процедур относится к классу комбинаторных задач дискретного математического программирования с булевыми переменными и нелинейными критериями и ограничениями. Для решения задач подобного типа пока не известно более эффективных алгоритмов, чем те, которые основаны на схеме ветвей и границ и реализуют частичный перебор допустимых решений. [24]

Отметим попутно, что удовлетворительная математическая теория, объясняющая причину столь малого числа базисных решений при практическом применении симплексного метода, до сих пор не разработана. Аналогично в рекуррентных соотношениях, используемых в методе динамического программирования, применяют принцип оптимальности, позволяющий устранить необходимость перебора всех допустимых решений. Эффективность этих методов оптимизации, основанных на частичном переборе, оправдывает постановку вопроса о поиске аналогичных подходов к решению задач целочисленного программирования. [25]

Ясно 1 что сформулированная выше задача & имеет 2П пробных планов. Основная черта аддитивного алгоритма, как и любого другого метода частичного перебора, состоит в получении оптимального плана ( или в выяснении отсутствия планов) путем рассмотрения лишь некоторого подмножества всех 2П пробных планов. Это осуществляется в рамках уже известной читателю общей схемы ветвления. [26]

К наиболее изученным задачам этого класса относятся целочисленные задачи линейного программирования, в которых на все переменные ( либо на их часть) наложено требование целочисленности. Один из наиболее эффективных методов решения задач целочисленного программирования - г - метод ветвей и границ, исходящий прежде всего из конечности числа планов задачи и использующий ее комбинаторные свойства. Центральную идею комбинаторных методов составляет замена полного перебора всех планов их частичным перебором. Это осуществляется отбрасыванием некоторых подмножеств вариантов, заведомо не дающих оптимума. [27]

Эта часть посвящена второй большой группе методов дискретного программирования. Центральную идею комбинаторных методов составляет замена полного перебора всех планов их частичным перебором. [28]

Страницы: 1 2