Большинство - метод - решение
Cтраница 1
Большинство методов решения ОДУ основано на задаче Коши, алгоритмы и программы для которой рассматриваются в настоящей главе. [1]
Большинство методов решения обратной задачи представляет собой различные варианты метода последовательных, приближений, при котором с некоторой пробной потенциальной функцией решается прямая задача, и по результатам сравнения вычисленных и экспериментально определенных частот получается поправка к пробной функции. Процесс повторяется до тех пор, пока не будет достигнуто удовлетворительное согласие вычисленных и экспериментально определенных частот. Получение таким путем потенциальной функции, удовлетворительно воспроизводящей наблюдаемый спектр частот, обычно не представляет особых затруднений, однако этим решение обратной задачи не исчерпывается. Необходимо исследовать полученное решение на единственность. [2]
Для большинства методов решения функциональных задач в системах управления производством время решения и объем памяти пропорциональны числу анализируемых вариантов управления, а определение этого числа, как правило, не представляет затруднений. Аналогично обстоит дело и при использовании итерационных методов. Больше трудностей возникает при определении ошибки отклонения получаемого решения от оптимального для каждого элемента шкалы сложности, однако применение верхних граней оценок значительно упрощает этот процесс. [3]
Для большинства методов решения задачи синтеза оптимальных виброзащитных систем характерны следующие принципы: используется линейная динамическая модель с одной степенью свободы; для системы с двумя степенями свободы рассматриваются лишь частные случаи синтеза; учитывается не более одного ограничения; для одной и той же модели изменение спектральной плотности воздействия приводит к необходимости повторения процесса решения задачи. Например, для синтеза оптимальной системы с активным динамическим гасителем колебаний ( судовых механизмов и машин) был выбран метод минимально-квадратичной оптимизации, позволяющий синтезировать системы с наименьшим значением интегральной квадратичной ошибки при учете ограничений, накладываемых объектом. [4]
Отсюда вытекает идея, лежащая в основе большинства рабочих методов решения ОЗЛП - идея последовательных проб. Действительно, попробуем разрешить уравнения (9.1) относительно каких-нибудь т базисных переменных и выразим их через остальные к свободных. [5]
Отсюда вытекает идея, лежащая в основе большинства рабочих методов решения ОЗЛП - идея последовательных проб. Действительно, попробуем разрешить уравнения (9.1) относительно каких-нибудь т базисных переменных и выразим их через остальные k свободных. [6]
В этом параграфе мы рассмотрим задачу нахождения минимума функции одной действительной переменной. Эта одномерная задача нередко возникает в практических приложениях. Кроме того, большинство методов решения многомерных задач сводится к поиску одномерного минимума. [7]
Далее будет конкретно рассмотрена задача интерполирования. Ее выделение вызвано наличием непосредственных многочисленных приложений, а также и следующим обстоятельством. Аппарат интерполирования многочленами является важнейшим аппаратом численного анализа; на его основе строится большинство методов решения других задач; его роль в численном анализе аналогична роли разложения Тейлора в классическом анализе. [8]
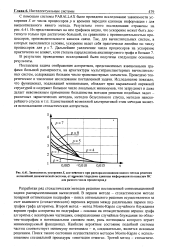 |
Зависимость ускорения 5, достигаемого при распараллеливании явного метода решения нелинейной динамической системы, от времени ( передачи единицы информации по каналам ВС. [9] |
Поставлена задача отображения алгоритмов, представленных взвешенными графами большой размерности, на архитектуры мультитранспьютерных вычислительных систем, содержащих большое число транспьютерных элементов. Проведено теоретическое и численное исследование поставленной задачи. Исследование показало, что функционал, подлежащий минимизации, обладает ярко выраженной овражной структурой и содержит большое число локальных минимумов, что затрудняет и даже делает невозможным применение большинства методов решения подобных задач - различных эвристических методов, методов безусловного спуска, методов наискорейшего спуска и т.п. Единственной возможной альтернативой этим методам является использование стохастических алгоритмов. [10]
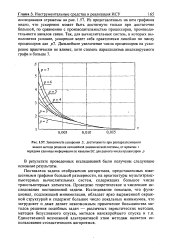 |
Зависимость ускорения S, достигаемого при распараллеливании. [11] |
Поставлена задача отображения алгоритмов, представленных взвешенными графами большой размерности, на архитектуры мультитранспьютерных вычислительных систем, содержащих большое число транспьютерных элементов. Проведено теоретическое и численное исследование поставленной задачи. Исследование показало, что функционал, подлежащий минимизации, обладает ярко выраженной овражной структурой и содержит большое число локальных минимумов, что затрудняет и даже делает невозможным применение большинства методов решения подобных задач - различных эвристических методов, методов безусловного спуска, методов наискорейшего спуска и т.п. Единственной возможной альтернативой этим методам является использование стохастических алгоритмов. [12]
Большинство задач геометрического проектирование являются детерминированными. Однако в рамках существующих на се годняшний день детерминированных методов глобальной оптимизации получить точное решение в задачах большой размерности не удается. В ряде работ, например [9, 26, 36, 37, 77, 90, 101, 146] и др. указывается, что при решении многоэкстремальных задач большой размерности поведение регулярных алгоритмов носит близкий к статистическому характер и использование-вероятностных подходов становится обоснованным. В основе большинства методов решения многомерных многоэкстремальных задач-лежит вероятностное описание свойств минимизируемого функционала. Эти свойства, как правило, заложены в распределении значений функционала при соответствующем задании вероятностной мерьв на области его определения. [13]
Страницы: 1