Большинство - приближенный метод
Cтраница 1
Большинство приближенных методов носит эвристический характер. Эвристическими принято называть методы, построенные на основе различных, подсказанных здравым смыслом соображений. Эти соображения, как правило, исходят из правдоподобных, но не обоснованных строго представлений о свойствах задачи. [1]
Большинство приближенных методов определения коэффициента газоотдачи пригодны лишь для однородных изотропных пластов. Использованные до настоящего времени технологии проектирования неоднородных залежей не позволяли с большой достоверностью прогнозировать продвижение воды по пропласткам. [2]
Большинство приближенных методов определения критического числа оборотов основывается на том, что - при критическом числе оборотов без воздействия внешних сил и без демпфирования возникают бесконечно большие прогибы вала, но отношение прогибов в различных точках вала остается неизменным. Поэтому в приближенных методах берут зл основу кривую прогибов, которая возникает яри статическом действии грузов, укрепленных на валу. [3]
В большинстве разработанных приближенных методов выражения, стоящие в числителе ( и знаменателе, если XF не нормирована), в конечном счете представляют в виде некоторой суммы одно -, двух -, трех -, четырех - и иногда многоцентровых кван-товомеханических интегралов. [4]
Следует особо отметить, что большинство приближенных методов исследования устойчивости регулирования нелинейных систем Б. В. Булгакова, А. Пуанкаре, Ван-дер - Поля, Л. С. Гольдфарба, Е. П. Попова, изображающих амплитудных кривых К. Магнуса, эквивалентного комплексного коэффициента усиления и другие базируются на методах малого параметра А. [5]
Как мы видели в предыдущих главах, для большинства приближенных методов математического анализа существуют оценки точности, позволяющие оценить по грешности полученных результатов. Для методов приближенного интегрирования дифференциальных уравнений дело обстоит значительно сложнее. Для некоторых методов точные оценки погрешности не существуют вовсе. [6]
Идея большинства приближенных методов состоит в отыскании такой линейной системы, свойства которой были бы близки к некоторым свойствам изучаемой нелинейной системы. Далее исследование нелинейной системы заменяется исследованием этой близкой линейной системы. [7]
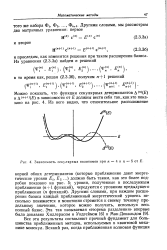 |
Зависимость секулярных полиномов при п 4ип 5от.. [8] |
Другими словами, при каждом расширении базиса каждый приближенный энергетический уровень несколько понижается и монотонно стремится к своему точному предельному значению, которое можно получить, используя весь полный базис. Все эти результаты составляют прочный фундамент для большинства приближенных методов, используемых в квантовой механике молекул. [9]
Однако этим дело не кончается: неясен вопрос о необходимых условиях типа принципа максимума для этого решения; ведь все выкладки § 5 были проведены на некоторой обычной траектории ( и ( -), () Это очень неприятное обстоятельство прежде всего для тех численных методов, которые основаны на прямом использовании принципа максимума. На первый взгляд оно не очень существенно для большинства приближенных методов решения вариационных задач, которые принципа максимума не используют ( точнее, используют его негативную формулировку), а состоят в построении минимизирующей последовательности управлений. [10]
Задача эта является весьма актуальной, так как, с одной стороны, подобного рода системы непосредственно появляются во многих задачах ( пространственные системы в строительной механике, нормальные уравнения в геодезии и астрономии), с другой стороны, к ним приводит применение большинства приближенных методов решения проблем высшего анализа - граничных задач для уравнений в частных производных и интегральных уравнений. [11]
Когда мы рассматриваем возможность дальнейшего сокращения числа слагаемых в разложении метода KB, отбрасывая конфигурации, которые, как представляется, дают незначительные вклады, ситуация значительно менее ясная. Наилучшими орбиталями, очевидно, будут такие, которые приведут к разложению относительно небольшой длины, но дающему хорошее приближение для функций в методе KB, что соответствует быстро сходящемуся разложению. Поскольку использование разложений метода KB ( явно или неявно) лежит в основе большинства используемых приближенных методов, то определение таких оптимальных орбиталей является одной из главных проблем вычислительной квантовой химии. Мы рассмотрим эту проблему ниже более подробно, здесь же только укажем на два традиционно установившихся способа выбора базисных орбиталей; полное обсуждение приближенных методов, которые при этом используются, дано в гл. [12]
Ее можно характеризовать остаточной ошибкой, которую нужно уменьшить. Остаточная ошибка зависит от вида функции, корень ( или максимум) которой определяется, и от ошибки начального приближения. Кроме того, большинство приближенных методов являются итерационными и поскольку практически используется небольшое число итераций, в частности для (8.2.6) - одна итерация, необходимо принимать во внимание и быстроту сходимости. В связи с этим следует отметить еще одно обстоятельство. [13]
Однако практические потребности не ограничиваются этими случаями. Очень часто возникает необходимость решения задач об охлаждении тел сложной конфигурации. Во всех перечисленных случаях температурное поле тела зависит от всех трех координат, и получить строгое аналитическое решение задачи становится невозможным. При сложной конфигурации тела весьма трудно также использовать большинство приближенных методов, которые очень эффективны в более простых случаях. [14]
В предыдущем параграфе было рассмотрено решение задачи об охлаждении тел трех простейших форм - плоской стенки, цилиндра и шара. Однако практические потребности не ограничиваются этими простейшими случаями. При этом температурное поле тела зависит от всех трех координат, и получить аналитическое решение становится невозможным. При сложной конфигурации тела весьма трудно также использовать большинство приближенных методов, которые очень эффективны в более простых случаях. [15]
Страницы: 1