Задача - штейнер
Cтраница 1
Задача Штейнера на евклидовой плоскости достаточно хорошо изучена [44, 24, 11, 12], и известно большое число свойств наикратчайшего дерева Штейнера. [1]
Евклидова задача Штейнера впервые была поставлена как геометрическая задача [13, 14, 44, 24], в которой нужно множество точек Р на евклидовой плоскости соединить линиями так, чтобы сумма длин отрезков была минимальна. [2]
В более позднем варианте задачи Штейнера на плоскости используется обычно линейное ( вместо евклидова) расстояние между точками. Такая постановка задач впервые была предложена Хэнном [28, 30] в связи с разработкой теории монтажа печатных схем электронных устройств. [3]
Нам представляется, что задачей Штейнера следует называть задачу Ламе с равными pj, а также ее мало исследованное обобщение: задана конечная совокупность точек плоскости, конечномерного или банахова пространства; требуется построить дерево ( граф) с наименьшей суммой длин ребер, множество концевых точек которого совпадает с совокупностью данных точек. [4]
В главе 7 рассматриваются задачи о деревьях, кратчайших остовах и задача Штейнера, а также приложения этих задач к проектированию электрических и газовых распреде ительных сетей. [5]
В главе 7 рассматриваются задачи о деревьях, кратчайших остовах и задача Штейнера, а также приложения этих задач к проектированию электрических и газовых распреде ител ьных сетей. [6]
Данная задача, представляющая и самостоятельный интерес, известна в литературе как задача Штейнера и для ее решения предложены достаточно эффективные численные методы. [7]
Интересно отметить, что в первой своей работе по трассировке электрических сетей авторы статьи [158] еще базируются на задаче Штейнера. В дальнейшем же [107, 159] они переходят к постановке, исходящей из задания не координат узлов, а именно исходной избыточной сети, и преобразуют ее затем в задачу на безусловный экстремум относительно контурных переменных. Для решения последней предлагаются обычный и усиленный методы покоординатной минимизации ( см. гл. [8]
Частный случай, когда R ( v) const, приводит к задаче построения кратчайшей связывающей сети, известной [12, 13] под названием задачи Штейнера. Отметим, что здесь R ( v) - pq ( v) зависит от структуры сети, но не от расположения дополнительных точек. [9]
При этих условиях можно легко показать [44], что если через каждую точку из множества Р провести вертикальные и горизонтальные линии, то решение задачи Штейнера можно получить, рассматривая в качестве возможных точек Штейнера точки пересечения полученной сетки линий. [10]
Если допускается на плоскости введение дополнительных искусственных вершин ( называемых точками Штейнера), то длину SST на множестве точек Р ID P можно уменьшить соответствующим подбором точек. Таким образом, для решения задачи Штейнера можно добавить в любых местах плоскости столько точек Штейнера, сколько необходимо для построения наикратчайшего дерева, стягивающего множество из Р точек. Получающееся наикратчайшее дерево называют наикратчайшим деревом Штейнера. [11]
Если допускается на плоскости введение дополнительных искусственных вершин ( называемых точками Штейнера), то длину 88Т на множестве точек Р гэ Р можно уменьшить соответствующим подбором точек. Таким образом, для решения задачи Штейнера можно добавить в любых местах плоскости столько точек Штейнера, сколько необходимо для построения наикратчайшего дерева, стягивающего множество из Р точек. Получающееся наикратчайшее дерево называют наикратчайшим деревом Штейнера. [12]
Эта задача, будем называть ее задачей Штейнера - Вебера, требует для некоторой точки на плоскости, чтобы она минимизировала весовую сумму расстояний до п заданных точек на плоскости. [13]
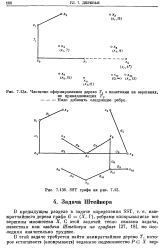 |
SST графа на. [14] |
С этой задачей тесно связана задача, известная как задача Штейнера на графах [27, 18], но последняя значительно труднее. [15]
Страницы: 1 2