Переход - оболочка
Cтраница 1
Переход оболочки в деформированное состояние связан со значительным изгибом в плоскости меридиана, о чем свидетельствует наличие геометрического ребра на соответствующем изометрическом преобразовании. Этот изгиб сопровождается появлением значительных напряжений растяжения-сжатия в срединной поверхности в направлении параллели. Из наглядных соображений мы заключаем, что деформация сильного изгиба на границе выпучивания и соответствующие деформации срединной поверхности для достаточно тонких оболочек должны иметь местный характер. [1]
Участок СА описывает переход оболочки из предельно устойчивого состояния к началу выворачивания. Участки ABf а затем BD характеризуют процесс полного выворачивания оболочки вплоть до образования сферического купола обратной кривизны. Заштрихованная площадь под характеристикой, как и в случае разрывных мембран, представляет собой работу на деформацию и разрушение хлопающей мембраны. [2]
При использовании бифуркационного критерия потери устойчивости ( в условиях мгновенного деформирования или ползучести) на каждом шаге по ведущему параметру решения ( прогибу, нагрузке или времени) после определения параметров, описывающих основное состояние оболочки, проверяем возможность перехода оболочки от основной осесимметричной к бесконечно близкой циклически симметричной форме, которой соответствует наличие ненулевых вещественных решений однородного вариационного уравнения (11.58) или системы Ритца (11.38) с коэффициентами (11.63), что имеет место при обращении в нуль определителя системы. Возможность бифуркации и форму потери устойчивости ( /) численно фиксируем по перемене знака определителя системы (11.38) на некотором шаге по ведущему параметру для некоторого номера гармоники /, который последовательно выбирается из заранее обусловленного диапазона целых чисел, начиная с нуля. [3]
При этом возникает возможность установить соотношение между силами и моментами, соответствующее переходу в пластическое состояние всех элементов по толщине заготовки или же пластической деформации всей оболочки, у которой изменяются продолные размеры и кривизна срединной поверхности. Тогда условие перехода оболочки в пластическое состояние может быть записано не соотношением между напряжениями в точке, а в виде конечного соотношения между силами и моментами, действующими в меридиональных и широтных сечениях оболочки. [4]
Полагаем, что переход оболочки в близкое к основному равновесное состояние происходит при неизменном значении параметра воздействия. [5]
При расчете напряжений во фланцах метод конечных элементов дает несколько нелинейную картину распределения напряжений, однако можно считать, что вычисленные по ним мембранные и изгибные ( линеаризованные) напряжения всегда близки к полученным приближенным методом. Наибольшие напряжения имеют место после приложения внутреннего давления в месте перехода оболочки крышки к верхнему фланцу. [6]
Удлинение 8ц е2, Y, углы поворота нормали О Ф2 и изменения кривизн х1 ( х2, х12, связанные с переходом оболочки в новое со-сотяние равновесия, выражаются через бифуркационные перемещения и, v, w с помощью линейных зависимостей, приведенных в § 6.3. Дальнейшее решение можно вести из условия б ( A3) 0 либо из условия А. На основе того и другого условия можно строить как точные, так и приближенные решения задач устойчивости оболочек. [7]
Переходы, сопровождающиеся большой интенсивностью поглощения ( излучения), происходят без изменения главного квантового числа электрона в молекуле. Такие переходы принято называть переходами внутривалентной оболочки. Среди этих последних различают два типа. [8]
В некоторый критический момент времени деформированная оболочка становится неустойчивой ( в смысле упругой устойчивости в большом) и мгновенно ( хлопком) переходит в новое, достаточно удаленное от основного состояние. Докритическое деформирование и хлопок происходят осесимметрично. Возможность потери устойчивости определяется наличием нетривиальных решений однородного вариационного уравнения, построенного относительно добавок к искомым функциям, соответствующих переходу оболочки в новое равновесное состояние. Для упрощения решений искомые функции в вариационных уравнениях аппроксимированы полиномами в первом приближении. [9]
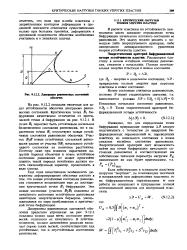 |
Диаграмма равномсных состояний оболочек. [10] |
На рис. 9.12.2 показана типичная для задач устойчивости оболочек диаграмма равновесных состояний. Критическая точка BI бифуркации качественно отличается от критической точки А бифуркации на рис. 9 - 12.1. В точке В перестает быть устойчивым начальное безмоментное состояние равновесия, но в окрестности точки В отсутствуют новые устойчивые состояния равновесия оболочки. Участок В В новых устойчивых состояний равновесия удален от участка QB начального устойчивого состояния на конечное расстояние. Поэтому даже при плавном нарастании нагрузки переход оболочки в новое устойчивое состояние равновесия не может произойти плавно; такой переход неизбежно должен носить скачкообразный характер, происходить в виде хлопка. [11]
Первый связан с интенсивным ростом скорости изменения прогиба оболочки в период времени, близкий к критическому. Второй критерий связан с мгновенной бифуркацией форм равновесия оболочки при ползучести в критический момент времени. Удовлетворение его проверяется на основе анализа вариационного уравнения устойчивости технической теории гибких оболочек, содержащего функции основного состояния. Независимому варьированию подвергаются малые добавки прогиба и функции усилий, связанные с переходом оболочки в соседнее равновесное состояние. Эти критерии являются результатом обобщения критериев потери устойчивости при мгновенном деформировании на случай ползучести. [12]
Страницы: 1