Перспектива - прямая
Cтраница 1
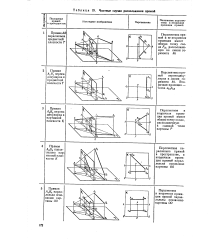 |
Частные случаи расположения прямой. [1] |
Перспектива прямой перпендикулярна к линии горизонта АЛ. [2]
Дана перспектива прямой L произвольного направления. Требуется провести через заданную точку Asa прямую, параллельную прямой L ( рис. 144), не продолжая прямую за рамку картины. [3]
Для построения перспективы прямой достаточно построить две точки, принадлежащие этой прямой. [4]
Рассмотрим построение перспективы прямой АВ. Для этого ( рис. 246 а), опустив перпендикуляр из точки F на плоскость Т, найдем точку / - основание точки схода, лежащую на прямой Тк, и соединим ее с точкой с. Прямая с / параллельна прямой CF, а следовательно, и прямой АВ. Восставив из точки / перпендикуляр к прямой Тк до пересечения с горизонтом НЯ, получим точку F. [5]
На рис. 342 перспектива прямой АВ и ее вторичная проекция определены перспективами и вторичными проекциями двух ее точек А к В. [6]
На картине задана перспектива прямой АВ ( рис. 404), предельная точка F которой находится за рамкой картины. Требуется через заданную перспективу точки 3 провести прямую MN, параллельную АВ. Для этого построим треугольник 1 - 2 - 3 произвольной формы, одну вершину которого расположим на линии горизонта в точке 2, а две другие на прямых АВ и MN. Из точки 2 проведем прямую, параллельную прямой 2 - 3, до пересечения с прямой, проведенной из точки 1 параллельно прямой 1 - 3, получим точку i. Таким образом, получим два подобных треугольника / - 2 - 3 и / 1 - 2 - Зь Центром подобия их является точка F, общая для всех прямых, параллельных прямой АВ. Соединив прямой точки 3 и 3 ], получим прямую MN, параллельную прямой АВ. [7]
Прямая будет вторичной проекцией полной перспективы NF прямой. [8]
Точка М, в которой перспектива прямой пересекает вторичную проекцию, является перспективой горизонтального следа прямой. [9]
Отметим точку, в которой перспектива прямой А В пересекается с основанием картины. [10]
Прежде чем перейти к построению перспективы прямых, точек и плоскостей, рассмотрим некоторые положения геометрии, придающие необходимую общность закономерностям элементарной геометрии и новым понятиям бесконечно удаленных точек и прямых, с которыми при построении перспективы приходится встречаться. [11]
Лучи AS и BS ограничивают на полной перспективе прямой перспективное изображение А1В1 отрезка АВ. [12]
Соединив эту точку с D, мы построим перспективу прямой, пересекающую масштаб глубин в точке ау. [13]
Соединив эту точку с D, мы построим перспективу прямой, пересекающую масштаб глубин в точке аку. [14]
Если же прямая лежит в предметной плоскости, то перспектива прямой и ее вторичная проекция совпадают. [15]
Страницы: 1 2 3 4