Дислокационная петля
Cтраница 1
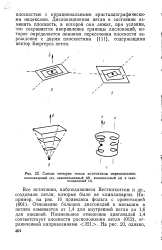 |
Схемы четырех типов источников переползания. [1] |
Дислокационная петля в состоянии изменить плоскость, в которой она лежит, при условии, что сохраняется направление границы дислокаций, которое определяется линиями пересечения плоскости зарождения с двумя плоскостями 111, содержащими вектор Бюргерса петли. [2]
Образовавшаяся дислокационная петля под действием своего линейного натяжения может расти или сокращаться посредством лереползания. [3]
Если дислокационная петля приобретает при своем распространении такие размеры, что доходит до свободной поверхности кристалла, то она, вырвавшись наружу, образует ступеньку, видимую на поверхности кристалла невооруженным глазом. Если же дислокационные петли выйти наружу не могут и должны оставаться внутри кристалла, то они будут оказывать сопротивление возникновению новых дислокационных петель и в конце концов источник перестанет действовать. [4]
Если дислокационная петля по окружности сечения замкнута, то, очевидно, угол закручивания равен нулю. [5]
 |
Ориентация круговой призматической петли относительно оси внешней нагрузки ( оси г. [6] |
Судьба дислокационной петли примерно такого радиуса целиком определяется ее ориентацией. [7]
Рассмотрим дислокационную петлю D в поле упругих напряжений а ь, созданных действующими на тело внешними нагрузками, и вычислим силу, действующую на нее в этом поле. Согласно общим правилам для этого надо найти работу 8RD, производимую над дислокацией при бесконечно малом ее смещении. [8]
Рассмотрим дислокационную петлю D в поле упругих напряжений Ofa, созданных действующими на тело внешними нагрузками, и вычислим силу, действующую на нее в этом поле. Согласно общим правилам для этого надо найти работу Шо, производимую над дислокацией при бесконечно малом ее смещении. [9]
При отрыве дислокационной петли от слабых точек закрепления дислокационная деформация сильно возрастает, причем этот рост происходит очень быстро. Величина дислокационной деформации определяется площадью, которую заметает дислокация при своем движении в плоскости скольжения. [10]
В противоположность призматическим и сидячим дислокационным петлям геликоидальные дислокации и источники переползания явдяются дислокационными дефектами, которые образуются при неоднородном выделении вакансий. Появление геликоидальных дислокаций или источников зависит главным образом от свойств исходной дислокации, которая может действовать как сток для вакансий. В принципе первоначальная дислокация, необходимая для образования геликоидальной дислокации или источника переползания, может быть создана призматическим выдавливанием. Однако некоторые из наблюдаемых геликоидальных конфигураций указывают на присутствие дополнительно наложенных сдвиговых напряжений. Целью этой статьи является обсуждение зарождения, роста и кристаллографии различных дислокационных дефектов, найденных в сплавах на основе алюминия после закалки и старения. Особое внимание было уделено прямому наблюдению дефектов с помощью электронной микроскопии на просвет и в особенности разнообразным дефектам, образующимся при аннигиляции сверхравновесных вакансий. [11]
 |
Геликоидальные дислокации, образовавшиеся при взаимодействии с вакансией и с межузельным атомом. [12] |
Если вектор Бюргерса дислокационной петли перпендикулярен к вектору Бюргерса скользящей частичной дислокации, то при реакции образуется дислокация с вектором Бюргерса, наклоненным к плоскости трансляционного двойника. [13]
 |
Геликоидальные дислокации, образовавшиеся при взаимодействии с вакансией и с межузельным атомом. [14] |
Если вектор Бюргерса дислокационной петли перпендикулярен к вектору Бюргерса скользящей частичной дислокации, то при реакции образуется дислокация с вектором Бюргерса, наклоненным к плоскости трансляционного двойника. [15]
Страницы: 1 2 3 4 5