Динамический анализ

Cтраница 2

Динамический анализ конструкции осуществляется по математической модели (3.1), включающей, кроме матрицы жесткости К, матрицу масс Af, а также матрицу С при учете диссипации энергии. [16]

Полный динамический анализ для многофазного течения остается нерешенной проблемой даже для строго однородных пластов. [17]

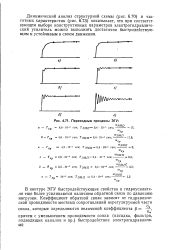Переходные процессы ЭГУ. [18]

Динамический анализ структурной схемы ( рис. 6.70) и частотных характеристик ( рис. 6.73) показывает, что при соответствующем выборе конструктивных параметров электрогидравлический усилитель можно выполнить достаточно быстродействующим и устойчивым в своем движении. [19]

Динамический анализ силовых установок обычно имеет многовариантный характер с целью выяснения влияния отдельных параметров на формирование исследуемых динамических характеристик установки. Для придания обозримости результатам сравнительного анализа число одновременно варьируемых параметров, как правило, не превышает одного-двух. Наиболее трудоемкие задачи анализа силовых установок с ДВС связаны с оценками их нагруженности при колебаниях, вызываемых регулярными возмущениями. Такие оценки требуют обычно многократного определения собственных частот н форм цепной динамической модели силовой установки на каждом шаге вариаций упругоинерционных параметров. [20]

Динамический анализ виброударного механизма состоит в определении перемещения и скорости ударной массы в функции времени в зависимости от конструктивных параметров и приложенных сил. [21]

Динамический анализ статистических данных о чрезвычайных ситуациях имеет большое значение в оценке общей эффективности деятельности по повышению безопасности жизнедеятельности и выявлению негативных тенденций, которые могут проявляться в ближайшем будущем. [22]

Динамический анализ следящих приводов с учетом нелинейных факторов целесообразно проводить на завершающем этапе проектирования. Это позволит внести последние коррективы в проект следящего привода и сократить затраты времени и средств на доводку экспериментального образца. [23]

Расчетная схема одноступенчатого зубчатого редуктора с прямозубыми цилиндрическими колесами. [24]

Динамический анализ зубчатых передач производится с учетом указанных выше факторов, причем из рассмотрения исключаются второстепенные явления, как: изменение угла зацепления зубьев вследствие их деформаций; влияние неравномерности распределения нагрузки по длине контактных линий и кромочного зацепления вследствие перекосов зубчатых колес под нагрузкой; проявление различных погрешностей изготовления и монтажа зубчатых колес. Эти факторы, оказывающиеся существенными при исследовании прочности или точности зубчатых передач, влияют и на динамические процессы в приводе. Однако их влияние имеет для привода в целом обычно локальный характер и при исследовании динамических свойств привода может не учитываться. [25]

Динамический анализ планетарных механизмов проводится при следующих допущениях. Предполагается, что одно - и двухступенчатые планетарные передачи имеют несколько ( 3, 4) симметрично расположенных сателлитов и что при динамических процессах в планетарном механизме нагрузка равномерно распределяется между сателлитами. Принятое допущение означает, что подшипники центральных колес не испытывают радиальных нагрузок и, следовательно, отсутствуют поступательные смещения центров инерции указанных колес при динамических процессах в планетарном механизме. [26]

Динамический анализ сейсмостойкости вышеуказанной модели, представленной в виде нелинейной системы с конечным числом степеней свободы, выполняется методами численного интегрирования системы дифференциальных уравнений движения. [27]

Динамический анализ ответа системы управления основан на использовании различных стимульных паттернов, или задающих функций, подаваемых на вход системы, и на оценке кинетики ответа. Установленные в этих исследованиях постоянные времени ответа колебались от нескольких секунд в случае первой фазы ответа в виде насыщения крови кислородом, 15 сут при реакциях на утомление и до 50 сут для второй фазы ответа на тренажные импульсы в случае плавательных движений. Исследование с применением ПСБП [20] оказалось особенно эффективным для выделения быстрой компоненты реакции насыщения крови кислородом в ответ на упражнение, а установленная постоянная времени ( 7 с) свидетельствует о том, что в процесс упражнения вовлечены нейронные пути. [28]

Динамический анализ ответа системы управления основан на использовании различных стимульных паттернов, или задающих функций, подаваемых на вход системы, и на оценке кинетики ответа. Установленные в этих исследованиях постоянные времени ответа колебались от нескольких секунд в случае первой фазы ответа в виде насыщения крови кислородом, 15 сут при реакциях на утомление и до 50 сут для второй фазы ответа на тренажные импульсы в случае плавательных движений. Исследование с применением ПСБП [20] оказалось особенно - эффективным для выделения быстрой компоненты реакции насыщения крови кислородом в ответ на упражнение, а установленная постоянная времени ( 7 с) свидетельствует о том, что в процесс упражнения вовлечены нейронные пути. [29]

Динамический анализ системы автоматического регулирования связан с исследованием ее поведения при нарушении равновесного режима. Нарушение равновесного режима может сопровождаться возвращением системы в исходное состояние, переходом ее в новое равновесное состояние, характеризуемое новым значением регулируемого параметра ( в статических системах), или непрерывным удалением от первоначального состояния. В первом и втором случаях система является устойчивой, в третьем - неустойчивой. [30]

Страницы: 1 2 3 4