Плоскость - изотропия
Cтраница 1
 |
Схема ориентации стекловолокон в плите ( а, в кольце ( б и в стержне ( в. [1] |
Плоскости изотропии параллельны оформляющим поверхностям. [2]
 |
Плоскости и оси. [3] |
Плоскостью изотропии является здесь плоскость, перпендикулярная волокнам. [4]
Ось, перпендикулярная плоскости изотропии, является осью симметрии бесконечного порядка, анизотропия материала определяется только различием между его свойствами в плоскости листа и в направлениях, не совпадающих с плоскостью листа. [5]
Пуассона, отнесенные к плоскости изотропии и направлению, перпендикулярному к ней. [6]
Пуассона, характеризующий сокращение в плоскости изотропии при растяжении в той же плоскости, v - коэффициент Пуассона, характеризующий сокращение в плоскости изотропии при растяжении в направлении, перпендикулярном этой плоскости, a v - коэффициент Пуассона, характеризующий сокращение в направлении, перпендикулярном к плоскости изотропии, при растяжении в плоскости изотропии, G, G - модули сдвига для плоскости изотропии и плоскостей, нормальных к плоскости изотропии соответственно. [7]
Пуассона, характеризующий сжатие в плоскости изотропии при растяжении в направлении армирования. [8]
Для транстропных материалов ( с плоскостями изотропии z - const) и изотропных материалов / 731 - 7з2 - Предположение о постоянстве межфазных параметров rj j достаточно жесткое - более реальной является их случайная зависимость от координат в межфазных плоскостях. Однако отказ от этого предположения, с одной стороны, сильно усложнил бы дальнейший анализ, а с другой стороны, поставил бы трудную проблему определения этих функций по имеющему место в действительности непрогнозируемому характеру распределения межфазных дефектов и несовершенств. [9]
Юнга для растяжения - сжатия в плоскости изотропии, Е0 - вдоль оси Оа3; v - коэффициент Пуассона, характеризующий поперечное сжатие в плоскости изотропии при растяжении в той же плоскости; v0 характеризует поперечное сжатие в плоскости изотропии при растяжении вдоль оси Оа3; G0 - модуль сдвига для плоскости, перпендикулярной плоскости изотропии. [10]
Плоскость 2 -, 3 является плоскостью изотропии. [11]
Плоскость плиты в этом случае является плоскостью изотропии, а ось, перпендикулярная ей, - осью симметрии бесконечного порядка. Такой материал называют поперечно ( аксиально) изотропным. Прочностные и упругие свойства материала в любом направлении в плоскости такой плиты будут эквивалентны между собой. [12]
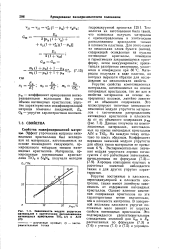 |
Зависимость модуля упругости материалов с хаотическим расположением нитевидных кристаллов Т1О2 ( / и А1N ( 2. [13] |
Упругие постоянные в плоскости, перпендикулярной к плоскости изотропии, также имеют линейную зависимость от содержания нитевидных кристаллов. Однако влияние изменения содержания кристаллов на эти характеристики менее значительно, чем в плоскости изотропии. В поперечной волокнам плоскости упругие постоянные мало зависят от упругих свойств нитевидных кристаллов. [14]
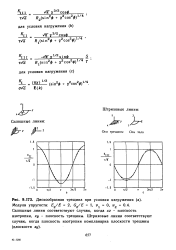 |
Дискообразная трещина при условии нагружения ( а. Модули упругости.. /. 2, С /. 1, у О, у. [15] |
Страницы: 1 2 3 4