Плоскость - начальная кривизна
Cтраница 1
Плоскость начальной кривизны совпадает с одной из главных плоскостей бруска и с плоскостью ху, в которой лежат действующие силы. Обозначим через z / t величину прогиба в каком-либо поперечном сечении, соответствующую начальному искривлению стержня. Через уг обозначим прогиб от действия приложенных к стержню сил. [1]
Соответствуют изгибу трубы в плоскости Начальной кривизны и изгибу из плоскости. В результате этого снижается изгибная жесткость и нарушается линейный закон распределения напряжений. [2]
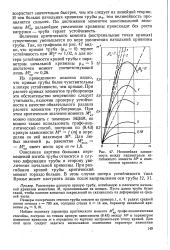 |
Нелинейная зависимость между параметрами изгибающего момента М и изменением кривизны т. [3] |
Рассмотрим длинную кривую трубу, изгибаемую в плоскости начальной кривизны моментами М, приложенными на концах. [4]
 |
Положение нейтральной линии и деформация сечений кривой трубы при изгибе. а - в плоскости кривизны трубы. б - из плоскости. [5] |
Долгое время считалось, что изгиб кривой трубы из плоскости начальной кривизны не вызывает сплющивание сечений и гибкость трубы при этом не увеличивается. Кармана [85], относящейся к плоскому изгибу, вышла работа И. [6]
В случае изгиба кривой трубы моментом, произвольно ориентированным относительно плоскости начальной кривизны, применяют оба решения, изложенные в данном параграфе. [7]
Изложенное в данном параграфе-решение для трубы с фланцами на концах относится к изгибу в плоскости начальной кривизны. В работе [26] показано, что аналогично решается задача и об изгибе из плоскости. [8]
В первой из рассматриваемых задач ( си.рис. I) арка шарнирно закреплена в плоскости и из плоскости начальной кривизны; концы ее защемлены от кручения; депланация торцов свободная. [9]
Из рис. 33 видно, что при изгибе из плоскости сечение трубы сплющивается в направлении под углом 45 к плоскости начальной кривизны. [10]
В работе [101] приводится обобщение решения задачи Кармана для случая изгиба кривой трубы моментом, плоскость действия которого перпендикулярна плоскости начальной кривизны труб. При внимательном рассмотрении характера деформации в этом случае можно убедиться, что здесь также имеет место сплющивание сечений, вызванное теми же причинами, что и в плоском изгибе. Если при изгибе в плоскости кривизны ( рис. 16 а) равнодействующие q продольных усилий направлены в сжатой зоне от центра кривизны оси трубы, а в растянутой - к центру, то при изгибе из плоскости ( рис. 16, б) возникают такие же силы q, направленные аналогично. Разница заключается лишь в положении растянутой и сжатой зон, так как нейтральная линия в случае изгиба в плоскости перпендикулярна этой плоскости, а при изгибе из плоскости - параллельна. В результате действия сил q и в том, и в другом случае круглое сечение трубы сплющивается, превращаясь в овальное. [11]
Криволинейный элемент пространственной системы трубопровода с самокомпенсацией температурных деформаций подвергается в общем случае действию равномерного внутреннего давления и изгиба в плоскости, произвольно ориентированной по отношению к плоскости начальной кривизны элемента. [12]
При этом не ставится вопрос о возможности выхода упругой линии из своей плоскости. Следовательно, имеется в виду, что гибкий стержень представляет собой тонкую полоску такой ширины, чтобы сохранялась плоская форма ее средней линии лри изгибе. Изогнутая тонкая полоска приобретает форму цилиндрической поверхности, при этом, однако, длина ее на порядок больше ширины, которая служит образующей цилиндрической поверхности. Такая полоска может быть первоначально прямой или криволинейной. Плоскость изгиба совпадает с плоскостью начальной кривизны средней линии полоски. [13]
Страницы: 1