Плоскость - окружность
Cтраница 1
Плоскости окружностей могут занимать в пространстве различные положения относительно плоскостей проекций. Часто они располагаются параллельно какой-либо плоскости проекций, как, например, окружности, вписанные в грани куба на фиг. [1]
Плоскость окружности вертикальна и ее цешр связан жестким стержнем длины а с фиксированным началом координат. [2]
Плоскость окружности АСВЕА ( acbea, а с Ь е а) параллельна плоскости V ( фиг. Горизонтальная проекция окружности - отрезок аЬ прямой линии, параллельный ОХ. На плоскость V окружность проектируется в истинную величину. [3]
Плоскости окружностей сечения перпендикулярны оси поверхности вращения, а центры окружностей принадлежат этой оси. Поэтому, если оси поверхностей вращения параллельны плоскости проекции, то на эту плоскость окружности сечения проецируются в отрезки прямых, перпендикулярных проекциям оси вращения. [4]
Поскольку плоскость окружности наклонена к плоскости проекции, то окружность проецируется в эллипс. [5]
Если плоскость окружности занимает произвольное положение по отношению к координатным плоскостям, то построение аксонометрической проекции окружности осуществляется так же, как это делается при построении аксонометрической проекции кривой ( см. с. [6]
В плоскости окружности К введем полярную систему координат с центром в центре окружности и полярной осью, направленной вертикально вниз. Точка М находится в поле силы тяжести P mg, направленной вертикально вниз. [7]
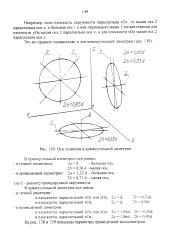 |
Оси эллипсов в прямоугольной диметрии. [8] |
Например, если плоскость окружности параллельна хОу, то малая ось 2 параллельна оси z, а большая ось 1 к ней перпендикулярна. [9]
 |
Система ко. [10] |
Примером может служить плоскость окружности, получаемой при пересечении соосных цилиндра и конуса с одинаковыми радиусами. [11]
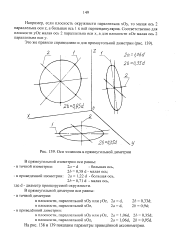 |
Оси эллипсов в прямоугольной диметрии. [12] |
Например, если плоскость окружности параллельна хОу, то малая ось 2 параллельна оси z, а большая ось 1 к ней перпендикулярна. [13]
Прямая, принадлежащая плоскости окружности и имеющая с окружностью только одну общую точку, называется касательной к этой окружности. [14]
Если прямая пересечения плоскостей окружностей ( С) и ( С) не пересекает окружность ( С), то можно подвергнуть, например, окружность ( С) предварительной гомотетии и привести одну из точек А этой окружности в точку А окружности ( С), расположенную на той же образующей. Доказательство проходит, даже если точки В и А совпадают, так как две касательные окружности, лежащие в различных плоскостях, принадлежат одной и той же сфере. [15]
Страницы: 1 2 3 4