Плоскость - зеркальное отражение
Cтраница 3
Известно, что молекулы, не имеющие элементов симметрии второго порядка ( плоскость зеркального отражения, центр инверсии и инверсионные оси), проявляют оптическую активность. Среди оптически активных молекул встречаются как низкосимметричные органические молекулы, так и различные кинетически инертные комплексы металлов. Все реакции, которые сопровождаются изменением их симметрии, ведут к изменению оптической активности. Таким образом, спектроскопия КД становится ценным методом изучения влияния растворителя. [31]
Пусть на чертеже дана группа симметрии С2г, с перпендикулярными к чертежу плоскостями зеркального отражения П ( JiCj и линией пересечения обеих этих плоскостей, являющейся осью второго порядка. Точки 7, 2, 3 и 4 являются эквивалентными в от ношении этой точечной группы. [32]
В группе Атт С 1 допустимые слои 2 [ 2ц ] накладываются плоскостями зеркального отражения; следовательно, эту группу исключаем. [33]
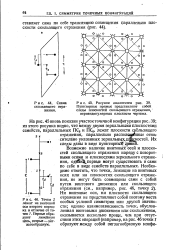 |
Схема скользящего отражения. [34] |
Возможно наличие винтовых осей и плоскостей скользящего отражения наряду с поворотными осями и плоскостями зеркального отражения, о дтйшЙ первые могут существовать и сами по себе в виде семейств параллельных. [35]
Каждая из них не имеет плоскости симметрии, но они связаны друг с другом плоскостью зеркального отражения; 6 - И.С. Бах: Искусство фуги, Контрапункт XVIII, отрывок; в-молекулы глицеринового альдегида; г - кристаллы винной кислоты. [36]
 |
Схема скользящего отражения.| Точки 2 лежат на винтовой оси второго порядка в отличие от точек 1. Первые образуют линейную цепь, вторые-зигзагообразную. [37] |
Возможно наличие винтовых осей и плоско стей скользящего отражения наряду с поворотными осями и плоскостями зеркального отражения, однако первые могут существовать и сами по себе в виде семейств параллельных. [38]
 |
Некоторые точечные группы на основе поворотной оси четвертого порядка. [39] |
Ось 4 ( в центре рисунка) направлена перпендикулярно плоскости рисунка; двойные линии - плоскости зеркального отражения, одинарные - поворотные оси второго порядка. [40]
Для описания точечной симметрии нужно рассмотреть только четыре типа элементов симметрии: центр симметрии, плоскость зеркального отражения, оси вращения и альтернирующие или инверсионные оси. К сожалению, для описания элементов симметрии используются две различные системы обозначений. Более поздней является система Германа - Могена, и ее, пожалуй, следует предпочесть, так как она одинаково пригодна для описания как точечной, так и пространственной симметрии. В кристаллографии обычно используется эта система. Однако более старая система описания точечной симметрии, предложенная Шенфлисом, не уступает системе Германа - Могена, и именно она применяется в спектроскопии, где, как правило, рассматривают только изолированные молекулы. [41]
 |
Некоторые точечные группы на основе поворотной оси четвертого порядка. [42] |
Ось 4 ( в центре рнсунка) направлена перпендикулярно плоскости рисунка; двойные линии - плоскости зеркального отражения, одинарные - поворотные осн второго порядка. [43]
В левой части рисунка изображена группа с поворотными осями второго порядка, параллельными оси У, плоскостями зеркального отражения, перпендикулярными этой оси. В точках их пересечения находятся центры инверсии. [44]
Ионы титана связываются друг с другом трансляциями а, Ъ, с, ионы кислорода - плоскостями зеркального отражения. [45]
Страницы: 1 2 3 4