Плоскость - площадка
Cтраница 2
Усилие должно быть приложено к краю площадки со стороны входного проема шахты перпендикулярно плоскости площадки. [16]
Последняя формула дает только величину касательного напряжения, но не указывает его направление в плоскости площадки. [17]
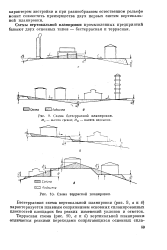 |
Схема бестеррасной планировки. Нс - высота срезки. НП - высота подсыпки.| Схема террасной планировки. [18] |
Бестеррасная схема вертикальной планировки ( рис. 9, а и б) характеризуется плавным сопряжением основных спланированных плоскостей площадок без резких изменений уклонов и отметок. [19]
Проекция Yy направлена нормально к площадке и называется нормальным напряжением; проекции Ху и Zy, лежащие в плоскости площадки, называются касательными напряжениями. [20]
Проекция вектора на нормаль к рассматриваемой площадке обозначается о и называется нормальным напряжением, а проекция вектора р на плоскость площадки обозначается т и называется касательным напряжением. Соответственно деформация, обусловленная нормальным напряжением и совпадающая с ним по направлению, обозначается е и называется нормальной, а деформация, обусловленная касательным напряжением, обозначается v и называется касательной деформацией или деформацией сдвига. Напряжения и деформации взаимно обусловлены и существуют только совместно. Согласно гипотезе о сплошности твердого тела напряжения и деформации являются непрерывными функциями координат. [21]
Проекция вектора р на нормаль к рассматриваемой площадке обозначается а и называется нормальным напряжением, а проекция вектора р на плоскость площадки обозначается т и называется касательным напряжением. Соответственно деформация, обусловленная нормальным напряжением и совпадающая с ним по направлению, обозначается е и называется нормальной, а деформация у называется касательной деформацией или деформацией сдвига. Напряжения и деформации взаимно обусловлены и существуют только совместно. Согласно гипотезе о сплошности твердого тела напряжения и деформации рассматриваются как непрерывные функции координат. [22]
Мы определим направление этой тангенциальной силы, задав две величины - две компоненты тангенциального напряжения - по двум взаимно перпендикулярным направлениям, лежащим в плоскости площадки AS. В общем случае произвольной деформации сила, действующая на площадку, может быть ориентирована как угодно. Чтобы определить ее величину и направление, нужно знать три компоненты этой силы по трем заданным направлениям. Для нахождения этих трех компонент нужно задать три величины - три компоненты напряжения на данной площадке: нормальную и две тангенциальные. Умножая их на величину площадки, мы и найдем три компоненты вектора силы, действующей на данную площадку, - нормальную и две тангенциальные. Таким образом, для того чтобы определить силу, действующую на данную определенную площадку, нужно знать три напряжения для данной площадки. Но площадки, служащие границами рассматриваемого элемента сплошного тела, могут быть расположены как угодно. Чтобы найти внешние силы, действующие на данный элемент, нам придется находить силы, действующие на любую площадку, находящуюся в данной точке тела, но произвольно ориентированную. Ясно, однако, что напряжение для данной площадки зависит от выбора площадки, к которой мы это напряжение относим. [23]
 |
Схема к определению напряжения в точке. [24] |
Полное напряжение на данной элементарной площадке может быть разложено по правилу параллелепипеда на три составляющих напряжения: одно по нормали к площадке - нормальное напряжение и два в плоскости площадки - касательные напряжения. [25]
Нормальным напряжением s и касательным напряжением т по данной площадке в рассматриваемой точке называются составляющая полного напряжения рп, нормальная к площадке, и, соответственно, лежащая в плоскости площадки, на которую оно действует. [26]
На экране, установленном перед площадкой, нанесите вертикальную линию О-О, которая соответствует вертикальной продольной плоскости симметрии трактора, и горизонтальную линию Б - Б на высоте h от плоскости площадки, на которой установлен трактор. [27]
Принимая эту схему, отвлекаются от наличия внутреннего трения, считая, что по площадкам соприкасания двух друг относительно друга движущихся объемов действуют лишь нормальные к площадке силы давления и полностью отсутствуют лежащие в плоскости площадки касательные силы. [28]
Принимая эту схему, отвлекаются от наличия внутреннего трения, считая, что по площадкам соприкасания двух друг относительно друга движущихся объемов действуют лишь нормальные к площадке силы давления и полностью отсутствуют лежащие в плоскости площадки касательные силы трения. [29]
Принимая эту схему, отвлекаются от наличия внутреннего трения, считая, что по площадкам соприкасания двух друг относительно друга движущихся объемов действуют лишь нормальные к площадке силы давления и полностью отсутствуют лежащие в плоскости площадки касательные силы. [30]
Страницы: 1 2 3 4