Плоскость - включение
Cтраница 1
 |
Эпюры напряжения при перестройке простого коаксиального резонатора. [1] |
Плоскость включения в резонатор конденсатора перестройки не должна совпадать с пучностью стоячей волны напряжения ни для одной из частот рабочего диапазона. В самом деле, при размещении конденсатора перестройки в пучности напряжения входное реактивное сопротивление последовательного контура на этой частоте должно быть бесконечным, что, как известно, физически невозможно выполнить. [2]
Сместим плоскость включения устройства связи с нагрузкой от края резонатора. [3]
Соответствующее значение / i определяет плоскость включения конденсатора перестройки с начальной емкостью Смнп, в которой перекрытие заданного диапазона волн ЯмаксДмин достигается при минимальном отношении Смакс / Смин конденсатора. [4]
Такой же ток / i протекает и в резонаторе рис. а слева от плоскости включения конденсатора С. [5]
Для композита с ориентированными пластинчатыми включениями вектор отклонений а направлен вдоль оси г3 перпендикулярно плоскости включений. Будем считать, что его координата оз распределена по равномерному закону на отрезке [ - Д Д ], где Д & Дтах, Дтах ( Н - Ь) / 2 ( Я и 6 - соответственно высота ячейки и толщина пластинчатого включения), с / Ь / Н есть величина объемного относительного содержания таких включений в композите. [6]
 |
Эпюры тока и напряжения в резонаторе с конденсатором перестройки во второй четверти ( а и в простом коаксиальном резонаторе ( б. [7] |
Случай включения конденсатора перестройки в третьей четверти рассматривать не будем, поскольку распределение токов в резонаторе в плоскости включения конденсатора перестройки не отличается от случая включения конденсатора перестройки в первой четверти. [8]
В главах 2 - 6 анализируются зависимости резонансной частоты, резонансного сопротивления и собственной добротности от характеристики ( характеристического сопротивления) и размеров коаксиального резонатора, от способа и плоскости включения в резонатор конденсатора перестройки частоты. Имеющиеся графики позволяют решить задачу синтеза резонатора и выбрать его оптимальные размеры, при которых резонансное сопротивление или добротность максимальны. Здесь приведен расчет конденсатора перестройки частоты в заданном диапазоне при минимальном перекрытии конденсатора по емкости с учетом возможности физической реализации. [9]
 |
Эпюры тока и напряжения в резонаторе с конденсатором перестройки во второй четверти ( синфазное распределение. [10] |
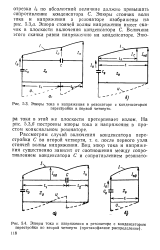
Длина 4 лежит в пределах - г - / а - гг - Эпюры стоячих волн тока и напряжения изображены на рис. 5.5 а. В плоскости включения конденсатора С наблюдается скачок на эпюре напряжения и излом эпюры тока. На рис. 5.5 6 построены эпюры тока и напряжения в простом коаксиальном резонаторе. [11]
Фаза стоячей волны тока постоянна вдоль всего резонатора. Эпюра тока в плоскости включения конденсатора С имеет излом. На рис. 5.4 6 построены эпюры тока и напряжения в простом коаксиальном резонаторе. [12]
Эпюры стоячих волн тока и напряжения в резонаторе изображены на рис. 5.3 а. Эпюра стоячей волны напряжения имеет скачок в плоскости включения конденсатора С. Величина этого скачка равна напряжению на конденсаторе. [14]
Параметрами кривых являются относительные длины lijl и kit. Очевидно, что графики ра ( РО характеризуют влияние плоскости включения в резонатор конденсатора С перестройки на эквивалентное сопротивление резонатора. На этих же рисунках кривая 1 соответствует случаю простого коаксиального резонатора. [15]
Страницы: 1 2