Любая плоскость

Cтраница 2

Любая плоскость в общем случае пересекает поверхности геометрических тел по плоской кривой или ломаной липни. Рассмотрим случаи пересечения плоскостью гранных тел и тел вращения. Часто такие сечения называют наклонными сечениями. [16]

Любая плоскость пересекает поверхность шара по окружности, если расстояние / от плоскости до центра шара меньше радиуса R шара. [17]

Любая плоскость - геометрическое место точек М, для которых AM tnU pV, где тир пробегают множество вещественных чисел, делит пространство на две выпуклые области, которые различают с помощью вектора W, дополняющего базис ( U, V плоскости. [18]

Любая плоскость делит пространство на две области, расположенные по разные стороны от этой плоскости. [19]

Любая плоскость пересекает поверхность шара по окружности, если расстояние / от плоскости до центра шара меньше радиуса R щара. [20]

Любая плоскость проекций первоначальной системы может быть заменена новой плоскостью, перпендикулярной незамененной плоскости. На комплексном чертеже первоначальную и вновь образованную системы плоскостей проекций обозначают осями проекций. [21]

Вне любой плоскости существуют точки. [22]

Поэтому любая плоскость, проходящая через прямую L, разбивает тетраэдр abed на две конгруэнтные части. [23]

Тогда любая плоскость II пространства А есть множество всех решений некоторой линейной системы. [24]

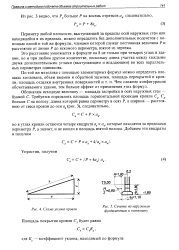Схема уклона кровли Площадь покрытия кровли С5 будет равна.| Сечение по наружным фундаментам и котловану. [25]

Периметр любой плоскости, выступающей за пределы осей наружных стен или находящейся в их пределах, можно определить без дополнительных подсчетов с помощью одной и той же формулы, членами которой служат постоянная величина Р и расстояние от линии Р до искомого периметра, взятое из чертежа. [26]

Сечение по свесу кровли.| Угол наружных стен здания. [27]

Периметр любой плоскости, выступающей за пределы осей наружных стен или находящейся в их пределах, можно определить без дополнительных подсчетов с помощью одной и той же формулы, членами которой служат постояннная величина Р и расстояние от линии Р до искомого периметра, взятое из чертежа. [28]

Положение любой плоскости в пространстве определяется тремя точками. В выбранной системе координат удобно в качестве трех опорных точек взять точки пересечения заданной плоскости с осями координат. [29]

В любой плоскости, параллельной обоим векторам ( двумерное направление которой х), таким образом, определяется - заданными двумя векторами), установим по ним определенную сторону вращения. Для этого центрируем векторы % и г 2 в точке О этой плоскости и представим себе, что вектор zt поворотом вокруг О на угол, меньший, приводится в совмещение с вектором яа по направлению и по стороне обращения ( фиг. [30]

Страницы: 1 2 3 4