Фронтальная плоскость - уровень
Cтраница 1
Фронтальные плоскости уровня, кроме плоскости Г, пересекают коническую поверхность по гиперболам, поэтому их также не следует применять в качестве вспомогательных секущих поверхностей. [1]
Фронтальные плоскости уровня, кроме проходящей через ось конической поверхности плоскости Г ( Г), пересекают эту поверхность по гиперболам. Значит их не следует применять в качестве вспомогательных секущих поверхностей. [2]
В качестве посредников Г выбираем фронтальные плоскости уровня, так как они, будучи параллельны плоскости параллелизма П2 коноида Ф, пересекают последний по образующим. [3]
Общая плоскость симметрии поверхностей является фронтальной плоскостью уровня, поэтому пересечение фронтальных очерков определяет опорные точки А ( А2) и В ( В2) линии пересечения. Это самая верхняя и самая нижняя точки линии. [4]
 |
Построение проекции сферы по заданной проекции окружности. [5] |
Общая плоскость симметрии поверхностей является фронтальной плоскостью уровня, поэтому пересечение фронтальных очерков определяет опорные точки A ( Az) и 8 ( 82) линии пересечения. Это самая верхняя и самая нижняя точки линии. [6]
Для построения линии пересечения используют в качестве посредников фронтальные плоскости уровня, которые пересекают шар по окружностям, а цилиндр - по образующим. [7]
А, В перемещаются по прямой 6 ( - вырожденной проекции фронтальной плоскости уровня 6, в которой перемещаются точки А, К. [8]
Для нахождения точек пересечения 2 и 3 ребер а и Ь со сферой использована фронтальная плоскость уровня ф, пересекающая сферу по окружности радиуса О / С - Затем найдены проекции точек 4 и 5, лежащих на фронтальном меридиане и определяющих видимость дуг эллипсов на фронтальной проекции. [9]
В итоге видим, что вспомогательные секущие сферы с центром в точке О и фронтальная плоскость уровня Г дают наиболее простые для построения на чертеже линии. [10]
Вторым плоскопараллельным движением р относительно ITj треугольник ABC преобразуем в треугольник ABC, расположенный во фронтальной плоскости уровня. [11]
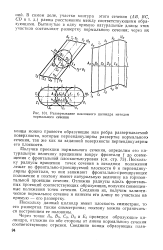 |
Развертывание наклонного цилиндра методом нормального сечения. [12] |
Получив проекции нормального сечения, определим его натуральную величину вращением вокруг фронтали f до совмещения с фронтальной плоскостью уровня ( см. стр. Поскольку радиусы вращения точек сечения в исходном положении лежат во фронтально-проецируемой плоскости 6 и перпендикулярны фронтали, то они занимают фронтально-проецирующее положение и поэтому имеют натуральную величину на горизонтальной проекции сечения. Отложив радиусы вдоль фронтальных проекций соответствующих образующих, получим совмещенные положения точек сечения. Соединив их, получим эллиптическое нормальное сечение и нанесем его длину по участкам на прямую - его развертку. [13]
При вращении точки А вокруг фронтально-проецирующей прямой i ( рис. 3.68) получим окружность, лежащую во фронтальной плоскости уровня. [14]
Очевидно, для решения этой задачи с успехом можно использовать в качестве посредников фронтально проецирующие плоскости, горизонтальные и ( или) фронтальные плоскости уровня. [15]
Страницы: 1 2