Бесконечная заряженная плоскость
Cтраница 1
Бесконечная заряженная плоскость имеет полусферический выступ. Найти поле и заряд, сосредоточенный на выступе. [1]
Бесконечная заряженная плоскость неожиданно приводится в поступательное движение. [2]
Если имеется бесконечная заряженная плоскость, плотность заряда которой равна q, то напряженность поля, создаваемого такой плоскостью, можно определить при помощи теоремы Остроградского - Гаусса. [3]
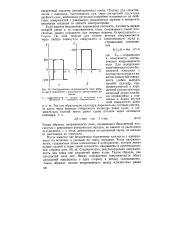 |
Распределение напряженности поля вблизи двух плоскостей с равномерно размазанным зарядом. [4] |
Пусть имеются две бесконечные заряженные плоскости с одинаковыми по величине и разными по знаку зарядами. Следовательно, результирующая напряженность для точек вне плоскостей равна нулю. [5]
 |
Распределение напряженности поля вблизи двух плоскостей с равномерно размазанным зарядом. [6] |
Пусть имеются две бесконечные заряженные плоскости с оди - q [ 2e ( наковыми по величине и разными по знаку зарядами. [7]
Таким образом, напряженность поля бесконечной заряженной плоскости пропорциональна поверхностной плотности заряда и не зависит от расстояния до плоскости. Следовательно, поле плоскости является однородным. [8]
По условию задачи поле создается бесконечной заряженной плоскостью и бесконечной заряженной линией. [9]
Определить напряженность электрического поля, которую создает бесконечная заряженная плоскость с поверхностной плотностью заряда а. Зависит ли напряженность поля плоскости от расстояния до плоскости. [10]
 |
К задаче. [11] |
В § 1.2 установлено, что напряженность электрического поля между двумя бесконечными заряженными плоскостями одинакова во всех точках. Учитывая это, для определения потенциала воспользуемся формулой (1.6), приняв потенциал отрицательной пластины равным нулю. [12]
Эта формула справедлива для любых радиусов R0, в том числе и для тех, которые стремятся к бесконечности. На расстоянии 6С С о участки сферической поверхности можно рассматривать как плоские. Силовые линии, всегда перпендикулярные к проводящей поверхности, в случае бесконечной заряженной плоскости будут параллельны между собой, а это означает, что поле не зависит от расстояния до пластины. [13]
Функция ф называется скалярным потенциалом. Нетрудно видеть, что скалярный потенциал определен с точностью до произвольной постоянной. Обычно ее определяют, требуя обращения в нуль потенциала на бесконечности. Это требование может быть выполнено, когда заряды расположены в ограниченной области пространства. В противном случае, например в поле бесконечной заряженной плоскости или нити, отсутствуют общепринятые требования выбора произвольной постоянной. [14]
Страницы: 1