Скользящая плоскость - симметрия
Cтраница 1
Скользящие плоскости симметрии включают трансляции вдоль одной из осей решетки, обычно на половину единичной трансляции с последующим отражением от оси скольжения. При составлении всевозможных комбинаций этих элементов симметрии получаются 230 различных пространственных групп. [1]
Примерами могут служить преобразования относительно скользящих плоскостей симметрии и винтовых осей. [2]
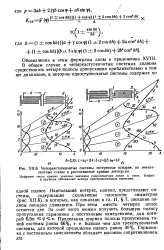 |
Четырехступенчатые системы встречные штыри, их эквивалентные схемы и рассчитанные кривые дисперсии. [3] |
Наибольший интерес, однако, представляют системы, содержащие скользящие плоскости симметрии ( рис. XII.6), в которых, как показано в гл. II, § 7, соседние полосы попарно сливаются. При этом вместо четырех полос остается две. [4]
 |
Попадание точки на скользящую плоскость симметрии или на винтовую ось. [5] |
Подчеркнем, что наличие геликогиры, равно как и скользящей плоскости симметрии, проходящей через центр тяжести точек, может быть обнаружено лишь, если точки обладают достаточно низкой симметрией. На этом примере вновь отчетливо видна важность учета собственной симметрии точек при исследовании подобных проблем. [6]
 |
Пространственные группы, подчиненные виду симметрии С. [7] |
Пространственная решетка может обладать либо только зеркальными плоскостями симметрии, либо только скользящими плоскостями симметрии, либо и теми и другими. [8]
На рис. 1.45, cud рассмотрен случай, когда точка лежит на скользящей плоскости симметрии. [9]
 |
Скользящая плоскость симметрии. [10] |
На рис. 1.55, cud рассмотрен случай, когда точка лежит на скользящей плоскости симметрии. [11]
В частности, как показано ниже, они сливаются в системах со скользящей плоскостью симметрии и с винтовой осью. [12]
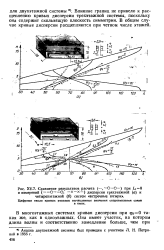 |
Сравнение результатов расчета ( - - О-О - при Z.. 0. [13] |
Влияние границ не привело к расщеплению кривых дисперсии трехэтажной системы, поскольку она содержит скользящую плоскость симметрии. В общем случае кривые дисперсии расщепляются при четном числе этажей. [14]
Найденное выше расположение электрических и магнитных стенок позволяет также несколько по-иному объяснить смыкание полос пропускания в системах со скользящей плоскостью симметрии. [15]
Страницы: 1 2