Проективная плоскость - порядок
Cтраница 1
Проективная плоскость порядка q, определенная аксиомами Ij, I2, I3, D, изоморфна плоскости Галуа. [1]
На проективной плоскости порядка 5 для любого овала существует 10 внутренних точек и 10 внешних прямых. [2]
Вопрос о существовании проективных плоскостей порядка п решен положительно только для пра, где р - аростое, а а - натуральное числа. [3]
Поскольку не существует проективной плоскости порядка шесть, искомый граф не существует. [4]
Можно показать, что проективная плоскость порядка 4 обязательно содержит овал А типа II. Всякое ребро определяет прямую. Для данной точки к не из А три прямые, проходящие через х и пересекающие А, определяют 1-фактор. Для данной прямой, не пересекающейся с пятью 1-факторов, определяемых ее точками, образуют 1-факторизацию. [5]
Если эта частичная геометрия не существует, то возможная проективная плоскость порядка 10 не содержит гиперовалов и, следовательно, не имеет расширений. [6]
Найти все значения п такие, что в проективной плоскости порядка п существуют полные 4-дуги. [7]
По теореме 12.3.3 аффинная плоскость порядка п существует тогда и только тогда, когда существует проективная плоскость порядка / г, и аффинная плоскость есть остаточная схема проективной плоскости. Но если мы возьмем проективную плоскость, то аффинные плоскости, полученные удалением двух различных прямых, будут изоморфны в том и только том случае, когда существует автоморфизм проективной плоскости, переводящий одну из этих прямых в другую. В самом деле, доказательство теоремы 12.3.3 показывает, что изоморфизм между аффинными плоскостями единственным образом можно распространить на изоморфизм между проективными плоскостями, в которые они вложены. [8]
Найти максимальное и минимальное числа Ki точек ( i 0, 1) для 6-дуги в проективной плоскости порядка ft, где t - чйсло секущих 6-дуги, проходящих через эти точки. [9]
В этой главе демонстрируется замечательное комбинаторное свойство числа 6, которое применимо для построения и доказательства единственности проективной плоскости порядка 4, графа Мура степени 7 и 5 - ( 12 6, 1) штейнеровой системы. Этот материал основан на лекциях Хигмана. [10]
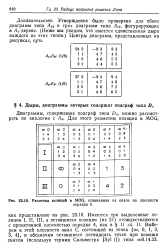 |
Разметка позиций в MOG, основанная на овале на плоскости. [11] |
Имеются три выделенные позиции I, II, III, а оставшиеся позиции ( их 21) отождествляются с проективной плоскостью порядка 4, как в § 11 гл. [12]
При v - п - - - п - - 1, / сге 1, Я1 ( v, k, Я) - конфигу-рацпя представляет собой проективную плоскость порядка п, являющуюся частным случаем конечной геометрии, содержащей конечное число точек и прямых с заданными условиями их инцидентности. [13]
Сорок два корня в 21д1 соответствуют точкам и прямым проективной плоскости порядка 4 и соединены по инцидентности, а 100 точек в 22t, i образуют граф Хигмана - Симса ( см. разд. [14]
Множество всех прямых, параллельных какой-либо одной прямой, называется классом. Считая такие классы идеальными точками, мы - следуя традиционному подходу - получаем проективную плоскость порядка q, ассоциированную с данной аффинной плоскостью. Однако аффинная плоскость, полученная из этой проективной; плоскости устранением какой-либо прямой, не обязательно изморфна исходной аффинной плоскости. [15]
Страницы: 1