Двойная касательная плоскость
Cтраница 1
Двойная касательная плоскость, катящаяся по р-у - Л - поверхности, определяет условия сосуществования фаз. Точки ( их две), в которых двойная касательная плоскость соприкасается с поверхностью, называются кодами. Геометрическое место нод называют бино-далью. [1]
Две точки касания, возникающие при обкатывании двойной касательной плоскостью, поверхности могут совпадать. [2]
Я 1 / 2, что означает наличие двух двойных касательных плоскостей. [3]
Прямая, соединяющая точки касания АО ( ХО, у0 z0) и А ( х, у, Zi) двойной касательной плоскости контура, служит образующей цилиндрической поверхности. [4]
Если к такой поверхности нельзя провести двойной касательной плоскости, то поверхность изображает состояние однофазной системы. [5]
Двойная касательная плоскость, катящаяся по р-у - Л - поверхности, определяет условия сосуществования фаз. Точки ( их две), в которых двойная касательная плоскость соприкасается с поверхностью, называются кодами. Геометрическое место нод называют бино-далью. [6]
Линии параболических точек исходной поверхности соответствует на двойственной поверхности ребро возврата. Особые точки на этой линии ( где она касается линии перегиба асимптотических) соответствуют ласточкиным хвостам. Линия самопересечения ласточкиного хвоста состоит из двойных касательных плоскостей исходной поверхности. Следовательно, в точке 7) сливаются две точки касания плоскости с исходной поверхностью, чем и заканчивается одно-параметрическое семейство двойных касательных плоскостей. [7]
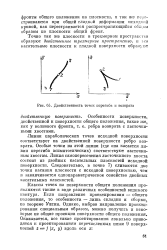 |
Двойственность точек перегиба и возврата. [8] |
Линии параболических точек исходной поверхности соответствует на двойственной поверхности ребро возврата. Особые точки на этой линии ( где она касается линии перегиба асимптотических) соответствуют ласточкиным хвостам. Линия самопересечения ласточкиного хвоста состоит из двойных касательных плоскостей исходной поверхности. Следовательно, в точке 7) сливаются две точки касания плоскости с исходной поверхностью, чем и заканчивается однопараметрическое семейство двойных касательных плоскостей. [9]
Линии параболических точек исходной поверхности соответствует на двойственной поверхности ребро возврата. Особые точки на этой линии ( где она касается линии перегиба асимптотических) соответствуют ласточкиным хвостам. Линия самопересечения ласточкиного хвоста состоит из двойных касательных плоскостей исходной поверхности. Следовательно, в точке 7) сливаются две точки касания плоскости с исходной поверхностью, чем и заканчивается одно-параметрическое семейство двойных касательных плоскостей. [10]
Линии параболических точек исходной поверхности соответствует на двойственной поверхности ребро возврата. Особые точки на этой линии ( где она касается линии перегиба асимптотических) соответствуют ласточкиным хвостам. Линия самопересечения ласточкиного хвоста состоит из двойных касательных плоскостей исходной поверхности. Следовательно, в точке 7) сливаются две точки касания плоскости с исходной поверхностью, чем и заканчивается одно-параметрическое семейство двойных касательных плоскостей. [11]
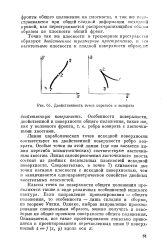 |
Двойственность точек перегиба и возврата. [12] |
Линии параболических точек исходной поверхности соответствует на двойственной поверхности ребро возврата. Особые точки на этой линии ( где она касается линии перегиба асимптотических) соответствуют ласточкиным хвостам. Линия самопересечения ласточкиного хвоста состоит из двойных касательных плоскостей исходной поверхности. Следовательно, в точке 7) сливаются две точки касания плоскости с исходной поверхностью, чем и заканчивается однопараметрическое семейство двойных касательных плоскостей. [13]
Страницы: 1