Единичная плоскость

Cтраница 3

В § 2.5 было отмечено, что в колориметрии удобно пользоваться проекциями цзетового треугольникам спектрального локуса, расположенными на единичной плоскости, на одну из координатных плоскостей или на некоторую другую плоскость. Форма этих фигур на единичной плоскости зависит от выбора основных цветов, а форма их проекций на выбранную плоскость - от метода проекции. [31]

Цветовой график представляет собой единичную плоскость ( X У Z 1) трехмерного цветового пространства. Векторы основных цветов пересекают единичную плоскость в вершинах цветового треугольника. [32]

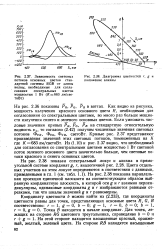Зависимость световых [ IMAGE ] Диаграмма цветностей г, g и. [33]

На рис. 2.38 показан спектральный локус и алихна в прямоугольной системе координату, г, аналогичной рис. 2.28. Цвета отдельных участков на этом локусе определяются в соответствии с данными, приведенными в гл. На рис. 2.38 показана параллельная проекция единичной плоскости на соответствующим образом выбранную координатную плоскость, в которой оси g и г взаимно перпендикулярны, одинаковые координаты g и г изображаются равными отрезками, так что шкалы значений g и г равномерны. [34]

Положение единичной плоскости определяется ортами R, G, В. В пространстве другой системы взаимонезависимых ортов R1G1B1 единичная плоскость не будет совпадать с единичкой плоскостью в системе ортов RGB и в общем случае не будет ей параллельна. [35]

Плоскость Q пересекает координатные оси в точках, соответствующих единичным количествам основных цветов и поэтому называется единичной. Поскольку трехцветные коэффициенты определяют положение точки данной цветности на единичной плоскости, их называют также координатами цветности. [36]

Единичная плоскость представляет для нас особый интерес. Важно отметить, что любой цветовой вектор S, или по крайней мере его продолжение, пересекает единичную плоскость в точке S. [37]

Уравнение (2.49), аналогичное (2.25), называется единичным и описывает единичную плоскость. Если X, У, Z - координаты R, G, В цвета соответственно, то (2.47) описывает единичную плоскость в цветовом пространстве. В - - - 1) и этой точке на единичной плоскости соответствует из (2.46) цветовой вектор Ц - В. Отсюда следует, что конец орта В лежит в единичной плоскости. [38]

Этот вектор лежит в плоскости нулевой яркости и пронизывает алихну в точке F. По мере увеличения длины волны вектор F будет перемещаться в пространстве, создавая коническую поверхность, след сечения которой единичной плоскостью образует кривую спектральных цветов - локус. Таким образом, локус является геометрическим местом расположения чистых спектральных цветов в плоскости цветового треугольника RGB. [39]

В нашей модели векторного пространства смешивание цветов соответствует сложению векторов. Sv S2 и S0 попадают на одну прямую - линию пересечения плоскости векторов ( S1; S2, S0) с единичной плоскостью. [40]

Геометрическая интерпретация трехкоординатного цветового пространства. [41]

О) и не лежат в одной плоскости; это соответствует тому, что ни один из основных цветов не может быть получен какой-либо смесью ( линейной комбинацией) двух других основных цветов. Один из целесообразных выборов масштабов основан на том, что равные количества К, Ст, В создают ахроматический цвет, соответствующий вектору ( Ж), который пересекает единичную плоскость R - - G - f В 1 в центральной точке N. [42]

В создают ахроматический цвет, соответствующий вектору S, который пересекает единичную плоскость ( рис. 1.4.4) в центральной точке. Точку 5 называют цветностью исследуемого цвета. Участок единичной плоскости, заключенный внутри цветового охвата данной системы цветовых координат, называют графиком цветности или цветовым треугольником. [43]

Выше указывалось, что выбор единичной плоскости произволен. Следовательно, в зависимости от ее выбора может быть несколько наборов индексов Миллера. В каждом из них единичные плоскости различны, что легко увидеть по отрезкам а, Ь, с, отсекаемым на кристаллографических осях, и данная плоскость hkl будет определяться различными индексами Миллера. [44]

Страницы: 1 2 3 4