Плотность - плазма
Cтраница 2
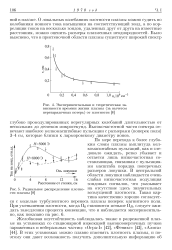 |
Экспериментальная и теоретическая зависимости времени жизни плазмы ( за вычетом.| Радиальное распределение плотно - на отсутствие здесь значительных сти плазмы возмущений плотности. Такая кар. [16] |
О локальных колебаниях плотности плазмы можно судить по колебаниям ионного тока насыщения на соответствующий зонд, а по корреляции токов на несколько зондов, удаленных друг от друга на известные расстояния, можно оценить размеры плазменных неоднородностей. [17]
Измерения электронной температуры и плотности плазмы путем анализа непрерывного спектра удается выполнить лишь в определенной области значений ве и Те, Редкая плазма излучает слишком мало света, чтобы измерения спектральной плотности в абсолютных единицах могли быть выполнены с необходимой точностью. При высокой плотности следует учитывать возможность самопоглощения. Имеющиеся экспериментальные данные показывают, что легко определяются значения пе в интервале 1015 - 1018 CM-S. Вряд ли можно надеяться на получение удовлетворительных результатов, если величина пе лежит ниже, чем 1013 сж-3. Область электронных температур в сотни и тысячи электрон-вольт хорошо поддается анализу. [18]
При возникновении пучково-плазменного разряда плотность плазмы лавинообразно нарастает. Она нарастаег до тех пор, пока это не вызовет уменьшение Те, после чего плотность плазмы достигает насыщения. [19]
Очевидно, при повышении плотности плазмы столкновения могут стать настолько частыми, что спонтанный распад перестанет быть единственным механизмом дезактивации. [20]
 |
Схема колебаний в магнитно-звуковом. [21] |
При уменьшении размеров объема или плотности плазмы нормальная фазовая скорость колебаний становится слишком большой, чтобы удовлетворить резонансному условию. При этом резонансные частоты стремятся к частотам аномальной дисперсии, близ которых фазовая скорость резко уменьшается. [22]
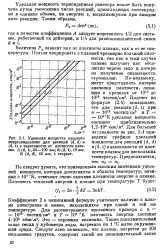 |
Удельная мощность ядерного знерговыделения дня реакций ( d, d и ( d, t в зависимости от плотности плазмы. 1 ( d, t, 50 - 100 кэе 2 ( d, t, 10 кз. 5 ( d, d, 60 кэв, t сгорает. [23] |
Величина Р0 зависит как от плотности плазмы, так и от ее температуры. Нельзя оперировать с плазмой чрезмерно большой плотности, так как в атом случае / / ( / t плазма излучает как абсолютно черное тело и потери на излучение оказываются огромными. Для большей наглядности на рис. 3.1 приведены графики удельной мощности для реакций ( d, d) л ( d, t) в зависимости от плотности плазмы для нескольких температур. [24]
 |
Блок-схема СВЧ-интерферометра. [25] |
Несравненно более совершенный метод определения плотности плазмы основан на перенесении в эту область частот интерферо-метрической методики. Соответствующая блок-схема изображена на рис. 23.3. Излучение от СВЧ-генератора делится на два канала: измерительный ж опорный. После прохождения через плазму или соответственно через волновод оба сигйала объединяются и детектируются. Как легко проверить, в случае квадратичного детектирования величина результирующего ( суммарного) сигнала зависит от косинуса разности фаз смешиваемых сигналов. [26]
Предположим сначала, что неоднородны как плотность плазмы, так и ее температура. В этом случае для регуляризации уравнения желобковых колебаний достаточно более полно учесть эффекты конечного ларморовского радиуса ионов. [27]
В лабораторных условиях плотность электронов ( плотность плазмы) обычна имеет величину порядка п0 1012 - 1016 см-3. Это значит, что сор б - 1010 - 6 - Ю12 сект1, так что типичная глубина проникновения для статических и низкочастотных полей лежит в пределах 5 - 10 1 - 5 - Ю 3 см. Вытеснение полей из плазмы - хорошо известный эффект в проблеме управляемых термоядерных реакций; имеются попытки его использования для удержания горячей плазмы ( см. гл. [28]
Зависимость среднего значения частоты ПРГ от плотности плазмы приведена на рис. 4.8. Там же представлена теоретическая зависимость ( сплошная линия), рассчитанная для усилителя, на вход которого подается спектр частот в полосе от 0 - т - 40 ГГц. Видно, что зависимость средней частоты от плотности плазмы в эксперименте хорошо совпадает с расчетом. Теоретическая кривая находится в хорошем соответствии с экспериментом. Незначительное расхождение наблюдается только в области высоких значений плотности плазмы. На рис. 4.8 также указана измеренная ширина спектра. [29]
Предположим сначала, что размеры и плотность плазмы таковы, что она находится в термодинамическом равновесии с излучением. В этом случае объемная плотность равновесного излучения, как известно, растет пропорционально четвертой степени температуры. [30]
Страницы: 1 2 3 4