Плотность - распределение - масса
Cтраница 2
Функция ф ( б) называется нормированной на 100 % плотностью распределения массы материала по диаметрам частиц или нормированной на 100 % дифференциальной функцией распределения. [16]
В уравнениях ( 10) - ( 18): р ( 1 - плотность распределения массы i - ro компонента в объеме жидкости; т - вязкость жидкости; g - ускорение силы тяжести; clp и с1я0 - относительные массовые концентрации компонента 1 в порах стенок канала соответственно при т т и т 0; cu Ir ci / o - относительные массовые концентрации компонента 1 в жидком потоке соответственно при T t и т: 0; d - половина расстояния между стенками канала; 8 - половина толщины стенок канала; остальные обозначения прежние. [17]
Средней плотностью какого-либо участка такой кривой называют отношение его массы к длине, а плотностью распределения массы кривой в данной точке называют предел средней плотности участка кривой, содержащего эту точку, при стягивании последнего к данной точке. [18]
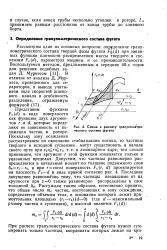 |
Схема к расчету гранулометрического состава фугата. [19] |
Рассмотрим один из основных вопросов: определение гранулометрического состава твердой фазы фугата F ( d) при заданных функции плотности распределения массы твердого в суспензии Fc ( d), параметрах машины и ее производительности. [20]
Простейшим примером, выходящим за границы статики, но хорошо известным из общего курса физики, является понятие о плотности среды, кратко выражающего, собственно говоря, слова: плотность распределения массы в сплошной среде. [21]
В любой точке непрерывности функции f ( x) имеем F ( x) f ( x), и потому функция / ( А:), - оо оо, называется плотностью распределения массы. [22]
Этим даны названия двум важнейшим геометрическим понятиям, которые в современной физике применяются на каждом шагу; достаточно будет очень немногих примеров, чтобы напомнить об их широком распространении. Плотность распределения массы, температура, потенциальная энергия в непрерывно протяженной системе, рассматриваемые каждая как функция места, являются примерами скалярного поля. Поле сил, в котором к каждой точке приложена определенная сила, является типичным примером векторного поля. Дальнейшими примерами являются в теории упругости поле сдвигов деформированного тела, если представить себе, что каждой точке отнесен отрезок, изображающий ее сдвиг, подобно этому в гидродинамике поле скоростей, наконец, в электродинамике электрическое и магнитное поля, в которых каждой точке отнесен определенный вектор электрической или магнитной напряженности поля. [23]
Согласно гипотезе сплошности масса среды распределена в объеме непрерывно и в общем неравномерно. Основной динамической характеристикой среды является плотность распределения массы по объему или просто плотность среды. [24]
Аналогично определяется выметание произвольной положительной меры, сосредоточенной на D. Вообще, если граница Г достаточно гладкая, то мера Ру абсолютно непрерывна и плотность распределения масс PJ, совпадает с нормальной производной Грина функции для D. При помощи моры ру решение задачи Дирихле записывается в виде так наз. [25]
Следовательно, интегральная сумма ( 1) приближенно равна массе т, заполняющей область V. Отсюда выводим физиче - ( ккй смысл тройного интегралам если / (, , v, z) есть неггрерив-ная плотность распределения массы в пространстве Сху. [26]
Кроме только что отмеченных двух основных и достаточно общих свойств сплошной текучей среды: 1) непрерывности распределения физических свойств и характеристик движения и 2) текучести, или легкой подвижности, при рассмотрении частных классов задач приходится - приписывать модели среды дополнительные макроскопические характеристики, определяющие ее индивидуальные материальные свойства, обусловленные действительными микроскопическими свойствами: молекулярной структурой и скрытыми движениями материи. В механике сплошных сред эти характеристики вводятся феноменологически, в форме заданных наперед констант или количественных закономерностей. Среди таких характеристик выделим, прежде всего, отражающие вещественные свойства среды при ее равновесном состоянии: молекулярный вес и плотность распределения массы ( или, короче, просто плотность среды), концентрацию примесей в многокомпонентных и многофазных смесях жидкостей, газов и твердых частиц, затем температуру и теплоемкость среды, электропроводность, магнитную проницаемость и другие физические свойства. [27]
Страницы: 1 2