Плотность - распределение - величина
Cтраница 1
Плотность распределения величины С называется законом Коши. [1]
Плотность распределения величины f называется законом Коши. [2]
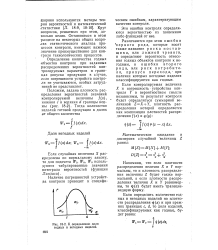 |
К определению доли годных и негодных изделий. [3] |
Напомним, что если плотности распределения величин X и У нормальны, то и плотность распределения величины Z будет также нормальной, а если плотности распределения величин X и У равномерны, то г з ( г) будет иметь трапециевидную форму. [4]
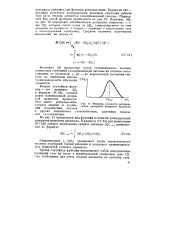 |
Функция плотности распределения резервной мощности промысла. [5] |
Первая из них - функция плотности распределения величины снижения добычи газа из-за отказов элементов газодобывающей системы. AQP, компенсируются за счет резервов на промысле, а справа - приводят к недоотпуску газа в магистральный газопровод. [6]
В § 21 ( распределение х2) мы нашли плотность распределения величины s при условии, что а и а заданы. [7]
Вероятное количество деталей Mt ( бй) определяем на основании известной функции плотности распределения величин приращения погрешности ( рис. 3.11) за время межремонтной наработки. [8]
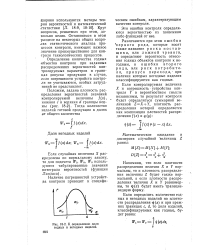 |
К определению доли годных и негодных изделий. [9] |
Напомним, что если плотности распределения величин X и У нормальны, то и плотность распределения величины Z будет также нормальной, а если плотности распределения величин X и У равномерны, то г з ( г) будет иметь трапециевидную форму. [10]
Кроме вышесказанного для расчета специфицированной нормы производственного запаса необходимо в рассматриваемом случае дополнительно использовать плотность распределения случайной двухмерной величины нормируемой марки материального ресурса у предприятия-потребителя. Здесь суммарный объем суточных отпусков за интервал поставки является факторным признаком, а объем поставки ( зависимый признак) - результативным. Между факторным и результативным признаками проявляется корреляционная связь. При такой связи на величину результативного признака оказывают влияние, помимо факторного, множество других признаков, действующих в различных направлениях одновременно или последовательно. [11]
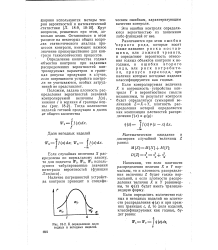 |
К определению доли годных и негодных изделий. [12] |
Напомним, что если плотности распределения величин X и У нормальны, то и плотность распределения величины Z будет также нормальной, а если плотности распределения величин X и У равномерны, то г з ( г) будет иметь трапециевидную форму. [13]
Рассмотрим сначала некоторые свойства плотности распределения случайной циклической величины, которые в конечном счете и обусловливают необходимость особого подхода к обработке выборки, состоящей из таких случайных величин. [14]
Как видим, это распределение уже не симметричное. Приведенные формулы ( 59), ( 61), ( 63) выражают плотность распределения величины Z через параметры распределений величин X и У. [15]
Страницы: 1 2