Плотность - распределение - вероятность - случайная величина
Cтраница 1
Плотность распределения вероятностей случайной величины имеет вид р ( х) уе 2 с. [1]
Плотность распределения вероятностей случайной величины имеет вид р ( х) уеах2 Ьх с. [2]
Что называется плотностью распределения вероятностей случайной величины. [3]
Уравнение (2.14) дает плотность распределения вероятностей случайной величины t в одноступенчатом реакторе. [4]
Как известно, плотность распределения вероятностей случайной величины по своим свойствам аналогична весовой функции, которая определяет систему ортогональных многочленов. В связи с этим устанавливается некоторое соответствие между наиболее важными законами распределения вероятностей и основными системами ортогональных многочленов. [5]
Функция известна как плотность распределения вероятностей случайной величины X ( рис. А. [6]
Функция ср ( лт) называется плотностью распределения вероятностей случайной величины X, произведение y ( x) dx - элементом вероятности. Кривая у ср ( дг) называется кривой распределения вероятностей данной случайной величины. [7]
Функция ф ( х) называется плотностью распределения вероятностей случайной величины X, произведение ф ( х) dx - элементом вероятности. Кривая у ф ( х) называется кривой распределения вероятностей данной случайной величины. [8]
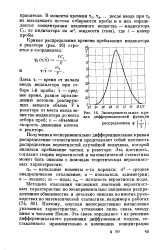 |
Экспериментальная кривая дифференциальной функции. [9] |
Полученная экспериментально дифференциальная кривая распределения статистически представляет собой плотность распределения вероятностей случайной величины, которой является пребывание частиц в реакторе. [10]
Полученная эмпирически дифференциальная кривая распределения статистически представляет собой плотность распределения вероятностей случайной величины, каковой является пребывание частиц в реакторе. Эта плотность, согласно теории вероятностей и математической статистики, может быть описана с помощью теоретических вероятностных характеристик. [11]
Доказать, что при п - - оо плотность распределения вероятностей случайной величины X сходится при любом значении аргумента х к плотности распределения вероятностей. [12]
Таким образом, для каждой весовой функции, являющейся плотностью распределения вероятности случайной величины, существует единственная ортогональная ( ортонормированная) система многочленов. [13]
Функцию р ( V) dF ( V) ldV называют плотностью распределения вероятностей случайной величины V, или ее дифференциальным законом распределения. [14]
Непрерывную случайную величину А следует задавать не указанием вероятностей ее отдельных значений, а непрерывной ( или кусочно-непрерывной) функцией р ( х), называемой плотностью распределения вероятностей случайной величины А. При этом вероятность того, что значения А находятся в промежутке от х до х А. [15]
Страницы: 1 2