Безразмерная плотность - тепловой поток
Cтраница 1
Безразмерная плотность теплового потока Q не зависит от т, поскольку в условиях радиационного равновесия плотность потока результирующего излучения qr в среде постоянна. Выражения (8.161) имеют тот же вид, что и (8.134) для серой среды. [1]
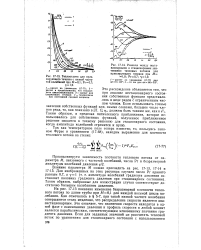
На рис. 17 - 13 показано изменение безразмерной плотности теплового потока по длине трубы при Af0 l для каждой восьмой цикла колебания. Как отмечалось в § 5 - 7, при такой низкой частоте колебания совершаются столь медленно, что распределение скорости является квазистационарным. Это означает, что изменения скорости находятся в одной фазе с изменениями давления и профиль скорости в любой момент является параболическим, соответствующим мгновенному значению градиента давления. [3]
Как видно из данных рис. 3.19, зависимости безразмерных плотностей тепловых потоков ( кривая 7) и безразмерной среднеобъем-ной температуры ( кривая 3) имеют хорошую качественную и количественную сходимость. Эти кривые можно описать одной зависимостью, которая будет характеризовать оба параметра с точностью до 10 % их значений в развитой стадии пожара. [4]
Здесь через q обозначен корень пятой степени локального значения безразмерной плотности теплового потока, подводимого из окружающей среды. Оказалось, что постоянные значения QBT 290 и Qsr 315 определяют соответственно начало перехода к турбулентности в динамическом и тепловом пограничных слоях. [5]
Здесь через g обозначен корень пятой степени локального значения безразмерной плотности теплового потока, подводимого из-окружающей среды. Оказалось, что постоянные значения QBT 290 и Qsr 315 определяют соответственно начало перехода к турбулентности в динамическом и тепловом пограничных слоях. [6]
При одностороннем лучистом нагреве плоских тел безразмерная плотность источника тепла в большинстве случаев является монотонно убывающей функцией х или может быть заменена безразмерной плотностью теплового потока на облучаемой поверхности. Когда начальное температурное поле равномерно по - х или Qt J монотонно уменьшается, то функция ff ( Ej, к ак правило, монотонно убывает. [7]
Ввиду того, что в большинстве случаев функции у, или г для начальной безразмерной избыточной температуры, безразмерной плотности источника тепла и безразмерной плотности теплового потока на облучаемой поверхности симметричны относительно координатных осей и, как правило, монотонно убывают с ростом абсолютного значения аргументов, безразмерная избыточная температура обычно достигает наибольших значений при у, 2, г в о. Когда соблюдается симметрия, во с увеличением абсолютного значения аргументов направления изменений функции начальной безразмерной избыточной температуры и других функций не совпадают, а также при наличии экстремумов или асимметрии каких-либо функций безразмерная избыточная температура может иметь экстремумы. [8]
Анализ наших опытов серий 3 - 5 показал, что для учета влияния величина тепловой нагрузки на теплообмен наиболее подходящим является параметр ( - Ц / бСр - безразмерная плотность теплового потока. Этот критерий подобия легко получается из уравнения для граничного условия, если температура на входе 7 [ и физические свойства при этой температуре приняты в качестве масштабов для температур и физических свойств. Этот параметр фигурирует также в [ б ], где дано численное решение задачи при фСОПЗЪ и переменных свойствах. Влияние этого параметра на теплообмен при синусоидальной нагрузке можно видеть на примере фиг. [9]
Интегральное уравнение ( - 11.4) было решено в работе [5] методом последовательных приближений, а также / в работе [9] с помощью метода неопределенных множителей, В работе [15] показано, что функция 0 ( t), характеризующая распределение температуры, и безразмерная плотность теплового потока Q могут быть точно рассчитаны с помощью метода Чандрасекара [1] и затабулированных им функций X и У. В табл. 11.1 приведены численные значения Q при различных оптических толщинах; при TO 3 0 Q можно рассчитывать сравнительно точно по асимптотической формуле, приведенной в сноске к таблице. [10]
Nua / gA и ReqH ( rpv) ( Q / nd) J ( rpv), и представляют графически на логарифмической бумаге в форме зависимости Nu / et i / ( Re), которую удобно интерпретировать в виде связи между безразмерным коэффициентом теплоотдачи и безразмерной плотностью теплового потока. Здесь же для сравнения представляют график подходящей теоретической зависимости из § 1.6. Практикума в той же системе координат. Следует обсудить в отчете степень согласования экспериментальных и расчетных данных, привлекая оценку погрешности опытов, указать причины возможных систематических погрешностей. [11]
Метод подобия дает следующую функцию для коэффициента сопротивления трения: - - - / ( Re, Рг, вг, Q, x / d, п, пс, п), где вш TW / T0 - безразмерная температура ( температурный фактор); Т0 - температура газа на входе ( масштаб температуры); Q qd / K0Ta - безразмерная плотность теплового потока. [12]
Дополнительные безразмерные числа могут появиться на основе граничных условий. Примерами могут служить число Эйлера Ей, представляющее собой безразмерный перепад давления, и число Дамке-лсра Da - безразмерная плотность теплового потока. [13]
Страницы: 1